Kurvendiskussion
Unter der so genannten Kurvendiskussion versteht man die Untersuchung von Funktionen mit Hilfe analytischer Mittel.
Dabei werden folgende Eigenschaften betrachtet: Nullstellen, Minima und Maxima (Hoch- und Tiefpunkte), Wendepunkte, Polstellen, Verhalten im Unendlichen. Die Ergebnisse einer solchen Kurvendiskussion erleichtern die Anfertigung einer Skizze des Graphen.
Nullstellen
Um die Nullstellen einer Funktion zu finden, berechnet man die Lösungsmenge der Gleichung . Wie man dabei im Detail vorgeht, hängt davon ab, welche Funktion man untersucht. Bei gebrochen rationalen Funktionen z.B. setzt man den Zähler = 0, um die Nullstellen der Funktion f(x) zu erhalten. Außerdem ist dann zu untersuchen, dass der Nenner verschieden von Null ist.
Ebenso ist es oft sinnvoll, den Schnittpunkt des Funktionsgraphen mit der -Achse zu bestimmen, also zu berechnen.
Extrempunkte
Um die Extrempunkte einer stetig differenzierbaren Funktion zu finden, setzt man die erste Ableitung von mit Null gleich (sog. notwendige Bedingung), das heißt, man berechnet die Lösungsmenge der Gleichung . Alle Lösungen sind mögliche Extremstellen. Erfüllt eine mögliche Extremstelle eine weitere (sogenannte hinreichende) Bedingung, z.B. dass die zweite Ableitung in dieser Stelle nicht 0 ist, dann handelt es sich um eine Extremstelle (siehe Satz 15VG). Genauer: Ist die zweite Ableitung größer als 0, handelt es sich um ein lokales Minimum, ist sie kleiner als 0, handelt es sich um lokales Maximum. Ist sie jedoch gleich 0, muss man weitere Untersuchungen anstellen, um zu entscheiden, ob eine Extremstelle vorliegt oder nicht.
Anschaulich bedeutet , dass an dieser Nullstelle die Tangente waagrecht verläuft, d.h. eine Steigung von "0" hat.
Historische Randbemerkung: Die Bestimmung der Extrema aus der Tangentensteigung wurde erstmals von Fermat vorgeschlagen (in einem Brief an Descartes), lange bevor es einen klaren Ableitungsbegriff gab.
Wendepunkte
Siehe: Wendepunkte.
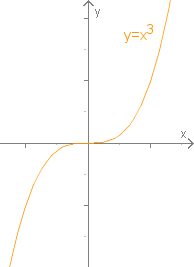
Sattelpunkte (auch: Terrassenpunkte)
Einen Wendepunkt mit zugleich waagerechter Tangente nennt man einen Sattelpunkt. Für ihn gilt demnach und , wie im Beispiel der Funktion mit der Gleichung
an der Stelle = 0.
Allerdings ist das kein hinreichendes Kriterium, es kann auch und werden, ohne dass ein Wendepunkt auftritt, wie im nachfolgenden Beispiel gezeigt.
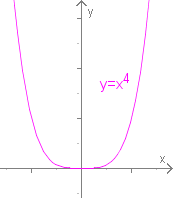
Erst wenn ist, ist ein Wendepunkt erwiesen; allgemeiner gilt: Es liegt ein Wendepunkt vor, wenn der Grad der ersten von 0 verschiedenen Ableitung ungerade ist; ist der Grad gerade, so handelt es sich um ein Extremum.
Polstellen
Um Polstellen zu finden, untersucht man, ob die Funktion Stellen enthält, an denen die Funktion nicht definiert ist. Die Polstelle ist dann aber von der Lücke ("Loch im Funktionsgraph") abzugrenzen. Ein hinreichendes Kriterium für eine Polstelle ist, dass die Nennerfunktion Null wird (also eine Nullstelle besitzt) und gleichzeitig die Zählerfunktion an dieser Stelle nicht Null wird. Das Kriterium ist aber nicht notwendig, da auch dann eine Polstelle vorliegt, wenn an einer Stelle die Zählerfunktion eine -fache Nullstelle aufweist und die Nennerfunktion an dieser Stelle eine mindestens (+1)-fache Nullstelle aufweist.
Verhalten im Unendlichen
Um das Verhalten im Unendlichen herauszufinden, untersucht man den Grenzwert der Funktion , wenn über alle Grenzen wächst, also gegen geht,
Dabei werden auch eventuell vorhandene Asymptoten bestimmt.
Die Mathematik ist eine Art Spielzeug, welches die Natur uns zuwarf zum Troste und zur Unterhaltung in der Finsternis.
Jean-Baptist le Rond d'Alembert
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Kurvendiskussion
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе