Beweis von Ungleichungen mittels Differentialrechnung

Die Kriterien für die Existenz von Extrema (Satz 15VG) und den Zusammenhang zwischen Monotonie und erster Ableitung (Satz 15VF) lassen sich für den Beweis von Ungleichungen verwenden.
ugl.png

Beispiel

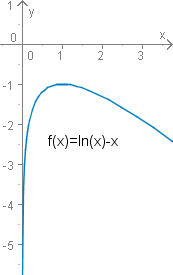
Man zeige ln⁡x≤x−1\ln x\le x-1 für x>0x>0. Die Funktion f(x)=ln⁡x−xf(x)=\ln x-x hat die erste Ableitung f′(x)=1x−1f'(x)=\dfrac 1 x -1. Ihr Wert ist für x<1x<1 positiv und für x>1x>1 negativ. Damit liegt das Maximum bei x=1x=1 mit dem Wert f(1)=−1f(1)=-1. Also gilt:
ln⁡x−x≤−1\ln x-x\le -1

Weiteres Beispiel

Wir wollen zeigen, dass
xp−px≤1−px^p-px\le 1-p(1)
für x≥0x\ge 0 und 0<p<10<p<1 gilt. Dazu betrachten wir die Funktion f(x)=xp−pxf(x)=x^p-px. Es ist f′(x)=p⋅xp−1−pf'(x)=p\cdot x^{p-1}-p =p(xp−1−1)=p(x^{p-1}-1). Nach Voraussetzung ist p−1<0p-1<0. Daher gilt f′(x)>0f'(x)>0 für 0<x<10<x<1 und die Funktion ist streng monoton wachsend. Für x>1x>1 ist f′(x)<0f'(x)<0 und ff ist monoton fallend. Sie nimmt für x=1x=1 ihr Maximum an mit f(1)=1−pf(1)=1-p. Daher gilt (1).
Ungleichung (1) können wir für die Herleitung weiterer wichtiger Ungleichungen verwenden.
Setzen wir x=abx=\dfrac a b mit a,b>0a,b>0 und q=1−pq=1-p dann schreibt sich (1) als: (ab)p−pab≤q\braceNT{\dfrac a b}^p-p\dfrac a b\leq q   ⟹  ap⋅b−p≤pab+q\implies a^p\cdot b^{-p}\le p\dfrac a b+q, woraus nach der Multiplikation mit qq folgt:

Formel 1661

apbq≤pa+qba^pb^q\le pa+qb für p+q=1p+q=1
Diese Formel kann man auf nn Faktoren (Summanden) erweitern:
Seien a1,…,an>0a_1,\dots,a_n>0 und p1,…,pn>0p_1,\dots,p_n>0 mit p1+⋯+pn=1p_1+\dots+p_n=1. Dann gilt:
a1p1⋅⋯⋅anpn≤p1a1+⋯+pnana_1^{p_1}\cdot\dots\cdot a_n^{p_n}\le p_1a_1+\dots+p_na_n(2)
Wir beweisen (2) durch vollständige Induktion.
Die Behauptung ist für n=1n=1 trivialerweise richtig.
Wir setzen s=p1+⋯+pns=p_1+\dots+p_n.
a1p1⋅⋯⋅anpn⋅an+1pn+1a_1^{p_1}\cdot\dots\cdot a_n^{p_n}\cdot a_{n+1}^{p_{n+1}} =(a1p1/s⋅⋯⋅anpn/s)s⋅an+1pn+1=\braceNT{a_1^{p_1/s}\cdot\dots\cdot a_n^{p_n/s} }^s\cdot a_{n+1}^{p_{n+1}}
≤(p1sa1+⋯+pnsan)s⋅an+1pn+1\le\braceNT{\dfrac {p_1} s a_1+\dots+\dfrac {p_n} s a_n}^s\cdot a_{n+1}^{p_{n+1}} (nach Induktionsvoraussetzung)
≤s(p1sa1+⋯+pnsan)+pn+1an+1\le s\braceNT{\dfrac {p_1} s a_1+\dots+\dfrac {p_n} s a_n}+ p_{n+1}a_{n+1} (nach Anwendung von (1) )
=p1a1+⋯+pnan+pn+1an+1=p_1a_1+\dots+p_na_n+ p_{n+1}a_{n+1} □\qed
 
 

Alles, was lediglich wahrscheinlich ist, ist wahrscheinlich falsch.

Rene Descartes

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Differentialrechnung