Extremalprobleme

Bei den Extremalprobleme (oder Extremwertaufgaben) geht es darum, die Extremwerte von Funktionen zu ermitteln. Diese Funktionen ergeben sich in der Regel erst durch Einbeziehung von Nebenbedingungen. Die Lösung der Probleme beruht auf der Anwendung von Satz 15VG.
Bei der Lösung von Extremalproblemen geht man in der Regel wie folgt vor:
  • Analyse der Problemstellung und Aufstellen der Funktionsgleichung der Extremalfunktion f(x)f(x) als reelle Funktion einer Veränderlichen
  • Berechnung der 1. Ableitung f′(x)f'(x)
  • Lösung der Gleichung f′(x)=0f'(x)=0. Die Lösungen sind die Kandidaten für die Extremalstellen.
  • Berechnung der 2. Ableitung f′′(x)f''(x) und Einsetzen der Extremalstellen, um sie als Minimum oder Maximum zu erkennen
  • Diskussion und Interpretation des Ergebnisses

Beispiel

Die obigen Schritte werden an einem einfachen Beispiel ausführlich erklärt.

Problem

Unter allen Rechtecken mit dem Umfang von 4\displaystyle{{4}} cm, ist das mit dem größten Flächeninhalt zu bestimmen.

Analyse

Wir bezeichnen mit aa und bb die Seiten des Rechtecks, mit AA seinen Flächeninhalt. Der Flächeninhalt des gesuchten Rechtecks soll maximal werden. Wir schreiben dafür
A=a⋅b→max⁡A=a\cdot b\rightarrow \max.(1)
In dieser Gleichung hängt der Flächeninhalt AA von zwei Größen (den Seiten aa und bb) ab. Um die Differentialrechnung (die für Funktionen einer Veränderlichen aufgestellt wurde) anwenden zu können, müssen wir eine Variable eliminieren. Dazu benutzen wir die im Problem gemachte Aussage über den Umfang.
Die Formel für den Umfang uu des Rechtecks ist
u=2a+2bu=2a+2b.(2)
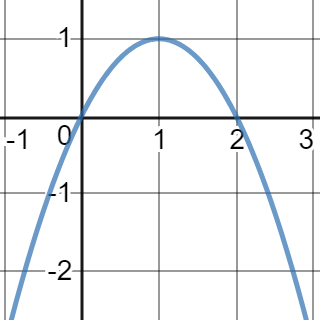
ReProblem.png
Graph der Funktion f(a)=2a−a2f(a)=2a-a^2
Aus der Aufgabenstellung ist u=4u=4 cm gegeben. Es gilt also: 4=2a+2b4=2a+2b, und damit a+b=2a+b=2, was wir zu
b=2−ab=2-a(3)
umformen.
Setzen wir dies nun in (1) ein, ergibt sich
A(a)=a(2−a)=2a−a2A(a)=a(2-a)=2a-a^2(4)
der Flächeninhalt als Funktion einer Seite.

Anwendung der Differentialrechnung

Um die Stellen zu bestimmen an denen AA ein Extremum annimmt, bestimmen wir die erste Ableitung von (4) nach der Variablen aa:
A′(a)=d⁡Ad⁡a=2−2aA'(a)=\dfrac{\d A}{\d a}=2-2a.(5)
Eine notwendige Bedingung dafür, dass die Funktion AA einen Extremwert annimmt, besteht darin, dass ihre erste Ableitung verschwindet, also
A′(a)=2−2a=0A'(a)=2-2a=0(6)
gilt.
Offensichtliche Lösung von (6) ist
a=1a=1.(7)
Um zu überprüfen, dass es sich bei der gefundenen Lösung von (6) tatsächlich um ein Maximum handelt, berechnen wir die zweite Ableitung von (4):
A′′(a)=−2A''(a)=-2,(8)
deren Wert immer negativ ist, womit es sich bei (7) um ein Maximum handeln muss.

Lösung

Schließlich bestimmen wir aus (3) b=1b=1, womit wir als vollständige Lösung ein Quadrat mit der Seitenlänge 1 erhalten.
Man kann diese Aufgabe natürlich auch allgemeiner lösen und erhält dann, dass unter allen Rechtecken mit vorgegebenen Umfang das Quadrat das flächengrößte ist.
 
 

Wer die erhabene Weisheit der Mathematik tadelt, nährt sich von Verwirrung.

Leonardo da Vinci

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Differentialrechnung