Infimum und Supremum

Definition Beschränktheit

Eine Teilmenge M⊆RM\subseteq \dom R heißt nach unten (oben) beschränkt, wenn es ein s∈Rs\in \dom R gibt, so dass s≤ms\leq m (s≥ms\geq m) für alle m∈Mm\in M. Dieses s s heißt untere (obere) Schranke. Eine obere (untere) Schranke ist also eine Zahl, die größer (kleiner) als alle Zahlen der vorgegebenen Menge ist.
MM heißt beschränkt, wenn MM sowohl nach unten als auch nach oben beschränkt ist.
 
 

Beispiele

Die Menge der reellen Zahlen ist nicht beschränkt. Denn für jede reelle Zahl aa gilt: a+1>aa+1>a. Damit ist es nicht möglich, eine obere Schranke zu finden.
Die Menge aller reellen Zahlen, die kleiner als 11 sind, ist nach oben beschränkt (11 ist eine obere Schranke) aber nicht nach unten beschränkt. Für diese Menge können wir auch formal
{a∈R ∣ a<1}\{a\in\domR \, |\, a<1\}(1)
schreiben.

Infimum und Supremum

Wenn MM nach unten beschränkt ist, dann heißt die größte untere Schranke Infimum und wird mit inf⁡M\inf M bezeichnet.
Wenn MM nach oben beschränkt ist, dann heißt die kleinste obere Schranke Supremum und wird mit sup⁡M\sup M bezeichnet.
Wenn das Infimum (Supremum) existieren, sind sie immer eindeutig bestimmt.
Wenn inf⁡M∈M\inf M \in M (sup⁡M∈M\sup M \in M) spricht man vom Minimum (Maximum) und schreibt min⁡\min bzw. max⁡\max.
Wenn M={a,b}M=\{a,b\} eine zweielementige Menge ist, kann man Minimum und Maximum direkt angeben.
max⁡{a,b}={awenn a≥bbwenn a<b\max\{a,b\}=\ntxbraceKO{ \array {a& {\text{wenn } a\geq b}\\ b &{\text{wenn } a<b}}} und min⁡{a,b}={awenn a≤bbwenn a>b\min\{a,b\}=\ntxbraceKO{ \array {a& {\text{wenn } a\leq b}\\ b &{\text{wenn } a>b}}}
Die in (1) definierte Menge hat 11 als Supremum, besitzt aber kein Maximum. Dass 11 obere Schranke ist, ist unmittelbar einsichtig. 11 ist aber auch die kleinste obere Schranke, denn jedes a<1a<1 gehört nach Definition zur Menge. Da 11 nicht zur Menge gehört, besitzt (1) kein Maximum.

Beispiel

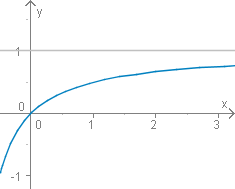
xx1.png
Graph von f(x)=x1+xf(x)=\dfrac{x} {1+x}
Die Menge M={x1+x∣x∈R;  x>0}M=\ntxbraceK{\dfrac{x} {1+x}\ntxbraceIO{ x\in\R ;\, \, x>0}} hat das Supremum 1. x1+x<1\dfrac{x}{1+x}<1 für alle x>0x>0, weil 1+x>01+x>0, also (1+x)−1>0(1+x)^{-1}>0 und somit aus x<1+xx<1+x folgt: x(1+x)−1<(1+x)(1+x)−1=1x(1+x)^{-1}<(1+x)(1+x)^{-1}= 1. Damit ist 11 obere Schranke von MM. Für jedes ϵ>0\epsilon >0 gilt: x1+x>1−ϵ\dfrac{x}{1+x}>1-\epsilon, falls x>1−ϵϵx>\dfrac{1-\epsilon}{\epsilon}, also z.B. für x=1−ϵϵ+1x =\dfrac{1-\epsilon}{\epsilon}+1. Daher ist 11 die kleinste obere Schranke (das Supremum). (Begründung für dieses Vorgehen in Satz 16LT (iii))
11 ist jedoch kein Maximum, weil stets x1+x<1\dfrac{x}{1+x}< 1 und daher 1∉M1\notin M .

Wir können das Maximum und Minimum wie folgt charakterisieren:

Satz 5828C

Es gilt a=max⁡Ma=\max M genau dann wenn, a∈Ma\in M und a≥ma\geq m für alle m∈Mm\in M.
Es gilt a=min⁡Ma=\min M genau dann wenn, a∈Ma\in M und a≤ma\leq m für alle m∈Mm\in M.

Beweis

Man wende die Definitionen an. □\qed
Das Maximum ist also das größte und das Minimum das kleinste Element einer Menge reeller Zahlen. Wie das obige Beispiel zeigt, müssen diese aber auch für beschränkte Mengen nicht existieren. Für endliche Mengen gilt jedoch:

Satz 5223B

Jede nichtleere endliche Menge M⊆RM\subseteq \dom R hat ein Maximum und ein Minimum

Beweis

Über vollständige Induktion nach der Anzahl der Elemente der Menge. Wenn MM nur ein Element hat, ist die Behauptung trivial. Das einzige Element ist Minimum und Maximum zugleich.
Habe MM jetzt n+1n+1 Elemente. Wir wählen ein beliebiges a∈Ma\in M aus und bilden T=M∖{a}T=M\setminus \{a\}. Diese Menge hat nn Elemente. Nach Induktionsvoraussetzung besitzt TT ein Maximum tmaxt_{max} und ein Minimum tmint_{min}. Wenn a>tmaxa>t_{max} sieht man sofort, dass aa Maximum von MM ist, andernfalls ist ebenso einsichtig, dass tmaxt_{max} Maximum von MM ist. Analog schließt man für das Minimum. Damit besitzt MM Maximum und Minimum. □\qed

Es ist unglaublich, wie unwissend die studirende Jugend auf Universitäten kommt, wenn ich nur 10 Minuten rechne oder geometrisire, so schläft 1/4 derselben sanft ein.

Georg Christoph Lichtenberg

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Zahlen