Wendepunkt

Ein Wendepunkt W(xW∣f(xW))W\left(x_W|f(x_W)\right) ist ein Punkt auf einem Funktionsgraphen, an welchem der Graph sein Krümmungsverhalten ändert. Ein Graph wechselt hier entweder von einer Rechts- in einer Linkskurve oder umgekehrt.
Dieser Wechsel wird auch Bogenwechsel genannt.
Die Ermittlung von Wendepunkten ist Bestandteil einer Kurvendiskussion.
Ein Wendepunkt an der Stelle xWx_W liegt vor, wenn die erste Ableitungsfunktion der differenzierbaren Funktion ff an der Stelle xWx_W ein relatives Extremum besitzt. Daraus lassen sich mehrere Kriterien zur Bestimmung von Wendepunkten einer Funktion ff ableiten.

Notwendiges Kriterium zur Bestimmung von Wendepunkten

Voraussetzungen:
1. ff ist bei xWx_W zweimal differenzierbar
2. xWx_W ist Wendestelle
f′′(xW)=0 f''(x_W)=0 \,

Hinreichende Kriterien zur Bestimmung von Wendepunkten

Die Funktion ff sei in einer Umgebung von xWx_W dreimal differenzierbar. Falls gilt f(xW)=0∧f′(xW)≠0f(x_W)=0 \wedge f'(x_W) \neq 0, so ist xWx_W Wendestelle. Wenn f′′′>0f''' > 0, dann ist xWx_W Rechts-Links-Wendestelle und wenn f′′′<0f''' < 0, dann ist xWx_W Links-Rechts-Wendestelle.
Falls die erste Ableitung an der Stelle xWx_W existiert und die zweite Ableitungsfunktion f′′(x)f''(x) an der Stelle xWx_W das Vorzeichen wechselt, so ist xWx_W ein Wendepunkt. Wenn f(xW)f(x_W) an xWx_W vom Positiven in das Negative wechselt, so ist xWx_W eine Links-Rechts-Wendestelle oder wenn f(xW)f(x_W) vom Negativen in das Positive wechselt, so ist xWx_W Rechts-Links-Wendestelle.
Ein Spezialfall der Wendestelle ist der Sattelpunkt.

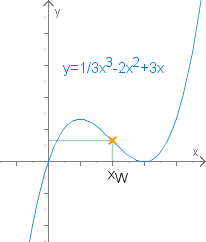
wpbsp1.png
Beispiel
f(x)=13⋅x3−2⋅x2+3⋅x { f(x) } = { \dfrac 1 3 } \cdot x^3 - 2 \cdot x^2 + 3 \cdot x
Dann ist die zweite Ableitung der Funktion:
f′′(x)=2⋅x−4 {f''(x)} = {2 \cdot x - 4}
Dann muss
f′′(x)=0=2⋅x−4 {f''(x)} = 0 = {2 \cdot x - 4}
gesetzt werden.
Das Ergebnis ist xW=2x_W=2.
Zugleich ist f′′′(x)=2 {f'''(x)} = 2 und daher ungleich 0, also handelt es sich um einen Wendepunkt.
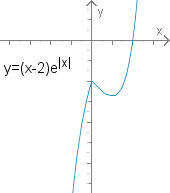
wpbsp2.png

Besondere Fälle

1. f(x)=(x−2)⋅e∣x∣ { f(x) } = (x-2)\cdot e^{|x|}
Der Graph dieser Funktion ändert bei x=0 sein Krümmungsverhalten (Übergang von Rechts- in Linkskrümmung).
Dennoch hat die Funktion bei x=0x=0 keinen Wendepunkt, da die erste Ableitung an der Stelle x=0x=0 nicht existiert.
Der Graph von f′f' hat daher für x=0x=0 kein Extremum.
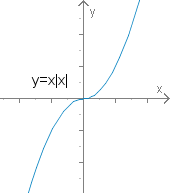
wpbsp3.png
2. f(x)=x⋅∣x∣ { f(x) } = x \cdot|x|
Diese Funktion besitzt in x=0x=0 einen Wendepunkt, obwohl die 2. Ableitung dort nicht existiert.
Jedoch hat der Graph der 1. Ableitungsfunktion f′f ' bei x=0x=0 ein Minimum.
 
 

Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Wendepunkt aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Anwendungen