Periodische Funktionen

Eine Funktion $f$ heißt periodisch, wenn eine reelle Zahl $\, p\in\domR$ existiert, so dass für alle ganzen Zahlen $k\in\domZ$ und alle $x\in\Domain f\,$ gilt:

Die Zahl $\, p$ heißt dabei Periode der Funktion.

Eine periodische Funktion durchläuft in gleichmäßigen Abständen die gleichen Wert. Das Verhalten der Funktion ist damit durch ihr Verhalten im Intervall $[0,\, p]$ eindeutig bestimmt. Alle Untersuchungen der Funktion können auf Betrachtungen in diesem Intervall beschränkt werden und dann auf den gesamten Definitionsbereich übertragen werden.

Wenn $\, p$ eine Periode ist, sind nach obiger Definition auch ganzzahlige Vielfache von $\, p$ Perioden. Man ist daher im Allgemeinen an der kleinsten Periode einer Funktion interessiert. Diese wird auch primitive Periode genannt. Allerdings wird der Begriff Periode vielfach auch synonym mit primitiver Periode gebraucht, man meint also die kleinste Periode, wenn man von Periode spricht.

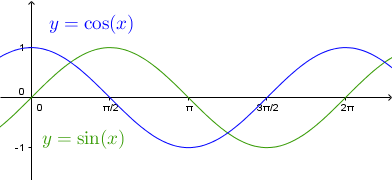
Typische Vertreter der periodischen Funktionen sind die Winkelfunktionen: Sinus, Kosinus und Tangens.

Ihre (primitive) Periode ist $2\pi$.