Definition der Winkelfunktionen am rechtwinkligen Dreieck

Ursprünglich sind die Winkelfunktionen als Seitenverhältnisse in rechtwinkligen Dreiecken und daher nur für Winkel von 0 bis 90 Grad definiert.
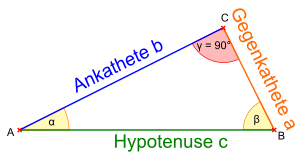
RechtwinkligesDreieck.png
Rechtwinkliges Dreieck mit Katheten aa, bb und Hypotenuse cc.
sin⁡α=Gegenkathete von αHypotenuse=ac \sin\alpha = \frac{\text{Gegenkathete von }\alpha}{\text{Hypotenuse}} = \frac{a}{c}
cos⁡α=Ankathete von αHypotenuse=bc \cos\alpha = \frac{\text{Ankathete von }\alpha}{\text{Hypotenuse}} = \frac{b}{c}
tan⁡α=Gegenkathete von αAnkathete von α=ab \tan\alpha = \frac{\text{Gegenkathete von }\alpha}{\text{Ankathete von }\alpha} = \frac{a}{b}
sin⁡β=Gegenkathete von βHypotenuse=bc \sin\beta = \frac{\text{Gegenkathete von }\beta}{\text{Hypotenuse}} = \frac{b}{c}
cos⁡β=Ankathete von βHypotenuse=ac \cos\beta = \frac{\text{Ankathete von }\beta}{\text{Hypotenuse}} = \frac{a}{c}
tan⁡β=Gegenkathete von βAnkathete von β=ba \tan\beta = \frac{\text{Gegenkathete von }\beta}{\text{Ankathete von }\beta} = \frac{b}{a}
 
 
Diese Definition ist unabhängig von der Wahl des rechtwinkligen Dreiecks, das zur Berechnung verwendet wird. In jedem rechtwinkligen Dreieck mit gleichem Winkel α\alpha ergeben diese Verhältnisse den gleichen Wert. Dies lässt sich z. B. mit den Strahlensätzen beweisen.
Aus diesen Beziehungen folgt unmittelbar die Beziehung:
tan⁡α=sin⁡αcos⁡α\tan\alpha = \frac{\sin\alpha}{\cos\alpha}
Die Ankathete des Winkels ist gleichzeitig die Gegenkathete des anderen spitzen Winkels β\beta des rechtwinkligen Dreiecks; da die Winkelsumme im Dreieck 180° beträgt, und der rechte Winkel 90° zu dieser Summe beiträgt, ist dieser Winkel β=90∘−α\beta = 90^\circ-\alpha und daher
cos⁡α=sin⁡(90∘−α)\cos\alpha = \sin(90^\circ-\alpha)

Gott existiert, weil die Mathematik widerspruchsfrei ist, und der Teufel existiert, weil wir das nicht beweisen können.

Andre Weil

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Trigonometrische Funktion aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Transzendente Funktionen