Diskussion der allgemeinen Sinusfunktion

Im Folgenden untersuchen wir den Verlauf der allgemeinen Sinusfunktion y=a⋅sin⁡(bx+c)y=a\cdot \sin(bx+c) in Abhängigkeit von den Parametern aa, bb und cc. Wir setzen dabei stets b≠0b\neq 0 voraus, da andernfalls die konstante Funktion y=a⋅sin⁡(c)y=a\cdot \sin(c) vorliegt.

Untersuchung der einzelnen Parameter

Wir untersuchen den Einfluss der einzelnen Parameter auf den Verlauf des Funktionsgraphen.
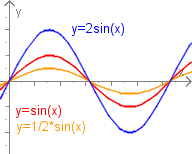
SinA1.png
 
 

b=1 und c=0

Für b=1b=1 und c=0c=0 nimmt die Funktion die Form y=a⋅sin⁡xy=a\cdot \sin x an. Der Wert von aa bestimmt dabei den maximalen und minimalen Wert von yy; die Sinusfunktion wird gestreckt oder gestaucht. Man spricht hierbei von der Amplitude, die sich ändert.
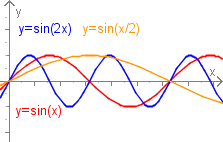
SinB.png

a=1 und c=0

Die Gleichung nimmt die Form y=sin⁡bxy=\sin bx an.
Durch Variation des Parameters bb verschieben sich die Nullstellen der Funktion und oder genauer es ändert sich die Anzahl der Nullstellen pro vorgegebenen Intervall. Bei einer Schwingung spricht man dann von der Frequenz.
Für b=2b=2 z.B. wird die Sinusfunktion schon im Intervall [0,π][0,\pi] vollständig durchlaufen.
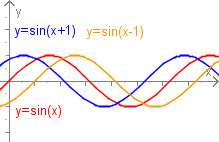
SinC.png

a=b=1

Die Gleichung nimmt die Form y=sin⁡(x+c)y=\sin(x+c) an.
Der Parameter cc bestimmt eine Verschiebung der Funktion entlang der xx-Achse.

Zusammenfassung

Die Parameter a,ba,b und cc der allgemeinen Sinusfunktion y=a⋅sin⁡(bx+c)y=a\cdot \sin(bx+c) bewirken folgende Änderungen des Funktionsverlaufs:
  • aa Stauchung oder Streckung in yy-Richtung
  • bb Stauchung oder Streckung in xx-Richtung
  • cc Verschiebung in xx-Richtung

Zusammenhang mit der Kosinusfunktion

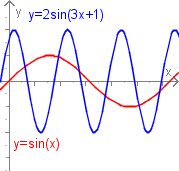
SinAll.png
Jede Gleichung der Form y=a⋅sin⁡(bx+c)y=a\cdot \sin(bx+c) kann in eine Gleichung der Form y=A⋅sin⁡bx+B⋅cos⁡bxy=A\cdot \sin bx+B\cdot \cos bx überführt werden und umgekehrt. Es gilt nach den Additionstheoremen a⋅sin⁡(bx+c)=a⋅(sin⁡bx⋅cos⁡c+cos⁡bx⋅sin⁡c)a\cdot \sin(bx+c)=a\cdot (\sin bx\cdot\cos c+\cos bx\cdot \sin c) =(acos⁡c)⎵=Asin⁡bx+(asin⁡c)⎵=Bcos⁡bx=\underbrace{(a\cos c)}_{=A}\sin bx+\underbrace{(a\sin c)}_{=B}\cos bx =Asin⁡bx+Bcos⁡bx=A\sin bx+B\cos bx.
Während der Übergang von a,b,ca,b,c zu A,B,bA,B,b sofort ersichtlich ist, ist auch die Umkehrung eindeutig möglich.
Im Fall B≠0B\neq 0 ermitteln wir cc wegen AB=cos⁡csin⁡c=cot⁡c\dfrac A B= \dfrac {\cos c}{\sin c}=\cot c aus c=arccot⁡ABc=\arccot\dfrac A B und können dann aa aus einer der beiden Gleichungen bestimmen. Für B=0B=0 haben wir bereits eine Gleichung nur mit der Sinusfunktion.

Seit der Zeit der Griechen bedeutet "Mathematik" zu sagen, "Beweis" zu sagen.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Transzendente Funktionen