Hyperbolische Funktionen

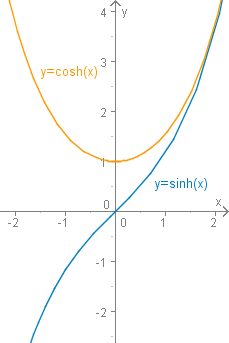
sincosh.png
Die hyperbolischen Funktionen sind wie folgt definiert
sinh⁡x=12(e⁡x−e⁡−x)\sinh x=\dfrac 1 2 (\e^x-\e^{\uminus x})
cosh⁡x=12(e⁡x+e⁡−x)\cosh x=\dfrac 1 2 (\e^x+\e^{\uminus x})
und heißen Hyperbelsinus (Sinus hyperbolicus) und Hyperbelkosinus (Kosinus hyperbolicus). Die Namen und Bezeichnungen rühren daher, dass ähnliche Beziehungen wie bei den trigonometrischen Funktionen gelten.
Man definiert analog zu den Winkelfunktionen den Hyperbeltangens (Tangens hyperbolicus) und Hyperbelkotangens (Kotangens hyperbolicus):
tanh⁡x=sinh⁡xcosh⁡x=e⁡x−e⁡−xe⁡x+e⁡−x\tanh x=\dfrac {\sinh x}{\cosh x}=\dfrac{\e^x-\e^{\uminus x}}{\e^x+\e^{\uminus x}}
coth⁡x=cosh⁡xsinh⁡x=e⁡x+e⁡−xe⁡x−e⁡−x\coth x=\dfrac {\cosh x}{\sinh x}=\dfrac{\e^x+\e^{\uminus x}}{\e^x-\e^{\uminus x}}

Eigenschaften

Funktion sinh⁡\sinh cosh⁡\cosh tanh⁡\tanh coth⁡\coth
Definitionsbereich R\dom R R\dom R R\dom R R∖{0}\dom R\setminus \{0\}
Wertebereich R\dom R [1,∞][1,\infty] ]−1,1[]-1,1[ R∖[−1,1]\dom R\setminus [-1,1]

Satz 5317A (Additionstheoreme für hyperbolische Funktionen)

  1. cosh⁡2x−sinh⁡2x=1\cosh^2x-\sinh^2x=1
    tanh⁡x⋅coth⁡x=1\tanh x\cdot\coth x=1
  2. sinh⁡(x1±x2)=sinh⁡x1cosh⁡x2±cosh⁡x1sinh⁡x2\sinh(x_1\pm x_2)=\sinh x_1\cosh x_2\pm\cosh x_1\sinh x_2
    sinh⁡2x=2sinh⁡xcosh⁡x\sinh 2x=2\sinh x\cosh x
  3. cosh⁡(x1±x2)=cosh⁡x1cosh⁡x2±sinh⁡x1sinh⁡x2\cosh(x_1\pm x_2)=\cosh x_1\cosh x_2\pm\sinh x_1\sinh x_2
    cosh⁡2x=sinh⁡2x+cosh⁡2x\cosh 2x=\sinh^2 x+\cosh^2 x

Beweis

Alle Behauptungen rechnet man durch Einsetzen der Definitionen nach. □\qed
Der Name hyperbolischen Funktionen kommt daher, dass sie zur Parametrisierung der Hyperbel x2−y2=1x^2-y^2=1 verwendet werden können wie man mit Hilfe von Satz 5317A (1) erkennt:
xx = cosh(t)(t), yy = sinh(t)(t).

Ableitungen

Die Ableitung des Sinus hyperbolicus lautet:
ddxsinh⁡(x)=cosh⁡(x)\frac{\mathrm{d}}{\mathrm{d}x}{\sinh}(x)={\cosh} (x).
Die Ableitung des Kosinus hyperbolicus lautet:
ddxcosh(x)=sinh⁡(x)\frac{\mathrm{d}}{\mathrm{d}x}{\rm cosh}(x)={\sinh} (x).
Die Ableitung der Tangens hyperbolicus lautet:
ddxtanh⁡(x)=1−tanh⁡2(x)\frac{\mathrm{d}}{\mathrm{d}x}{\tanh}(x)=1-{\operatorname{tanh}}^2 (x).

Umrechnung

Funktion sinh⁡ \sinh cosh⁡ \cosh tanh⁡ \tanh coth⁡ \coth
sinh⁡(x)= \sinh(x)= sinh⁡(x)  \sinh(x)\, sgn⁡(x)cosh⁡2(x)−1 \sgn(x)\sqrt{\cosh^2(x)-1} tanh⁡(x)1−tanh⁡2(x) \frac{\tanh(x)}{\sqrt{1 - \tanh^2(x)}} sgn⁡(x)coth⁡2(x)−1 \frac{ \sgn(x)}{\sqrt{\coth^2(x) - 1}}
cosh⁡(x)= \cosh(x)=  1+sinh⁡2(x) \,\sqrt{1+\sinh^2(x)}  cosh⁡(x) \,\cosh(x)  11−tanh⁡2(x) \, \frac{1}{\sqrt{1 - \tanh^2(x)}}  ∣coth⁡(x)∣coth⁡2(x)−1 \, \frac{\left| \coth(x) \right|} {\sqrt{\coth^2(x)- 1}}
tanh⁡(x)= \tanh(x)=  sinh⁡(x)1+sinh⁡2(x) \,\frac{\sinh(x)}{\sqrt{1+\sinh^2(x)}}  sgn⁡(x)cosh⁡2(x)−1cosh⁡(x) \,\sgn(x)\frac{\sqrt{\cosh^2(x)-1}}{\cosh(x)}  tanh⁡(x) \,\tanh(x)  1coth⁡(x) \,\frac{1}{\coth(x)}
coth⁡(x)= \coth(x)=  1+sinh⁡2(x)sinh⁡(x) \,\frac{\sqrt{1+\sinh^2(x)}}{\sinh(x)}  sgn⁡(x)cosh⁡(x)cosh⁡2(x)−1 \,\sgn(x)\frac{\cosh(x)}{\sqrt{\cosh^2(x)-1}}  1tanh⁡(x) \,\frac{1}{\tanh(x)}  coth⁡(x) \,\coth(x)
 
 

So seltsam es auch klingen mag, die Stärke der Mathematik beruht auf dem Vermeiden jeder unnötigen Annahme und auf ihrer großartigen Einsparung an Denkarbeit.

Ernst Mach

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen