Konstruktion der Winkelhalbierenden

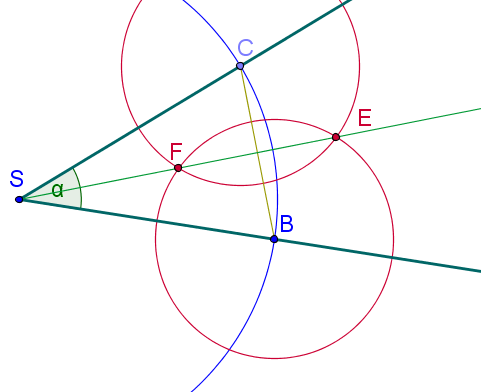
Ein Winkel $\alpha$ ist durch seine beiden Schenkel (Halbgeraden mit gemeinsamen Anfang im Scheitel des Winkels) gegeben. Dann kann die Winkelhalbierende mit Zirkel und Lineal (Geodreieck) konstruiert werden: Um den Scheitelpunkt $S$ wird ein Kreis mit beliebigem Radius gezeichnet. An den Schnittpunkten mit den Schenkeln des Winkels ($B$ und $C$) wird der Zirkel erneut angesetzt. Dann zeichnet man jeweils einen Kreis mit gleichem Radius. Die Schnittpunkte dieser zwei Kreise ($E$ und $F)$ liegen auf der Winkelhalbierenden. Die durch $S$, $E$ und $F$ gehende Gerade ist damit genau die Winkelhalbierende.

Bei dieser Konstruktion wird benutzt, dass die Winkelhalbierende zugleich Mittelsenkrechte in dem gleichschenkligen Dreieck $\triangle SBC$ ist, das durch den Scheitel und die zwei ersten Hilfspunkte gegeben ist.

Liegen allgemeiner zwei Geraden vor, die sich in einem Punkt schneiden, so haben wir vier Winkel und damit vier Winkelhalbierende. Die Winkelhalbierenden zweier Scheitelwinkel fallen zusammen; also bleiben nur zwei Winkelhalbierende übrig. Diese zwei Winkelhalbierenden - die zueinander orthogonal sind - nennt man die Winkelhalbierenden der zwei Geraden.

Wenn wir wieder zu dem Fall eines Winkels zurückkommen, der von zwei Schenkeln (Halbgeraden) begrenzt wird, und nun diese Schenkel zu Geraden verlängern, dann bekommen wir zwei Geraden mit zwei Winkelhalbierenden. Die eine davon ist die Winkelhalbierende des ursprünglichen Winkels; die andere ist die Winkelhalbierende seines Nebenwinkels; sie heißt Außenwinkelhalbierende des ursprünglichen Winkels.