Kathetensatz im rechtwinkligen Dreieck

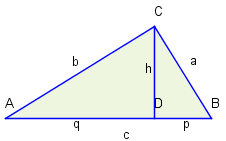
DreieckRwPq.png
Rechtwinkliges Dreieck mit Bezeichnungen
In einem rechtwinkligen Dreieck ΔABC\Delta ABC sei cc die Hypotenuse und a,ba,b die beiden Katheten; DD der Fußpunkt der Höhe hh durch CC. Mit pp und qq werden die beiden Hypotenusenabschnitte DB‾\overline {DB} und AD‾\overline {AD} bezeichnet. Es gilt:
a2=pca^2=pc und b2=qcb^2=qc
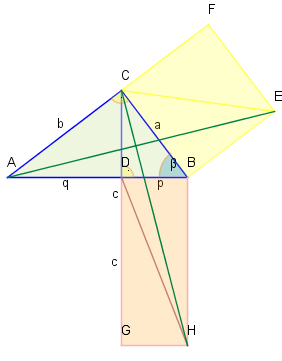
KatBew.png
Zum Beweis des Kathetensatzes

Beweis

Um die Flächengleichheit der Vierecke BEFCBEFC und DGHBDGHB zu zeigen, genügt es, die Dreiecke BECBEC und BDHBDH zu betrachten. Die Dreiecke BECBEC und ABEABE haben den selben Flächeninhalt, da sie in der Seite BEBE und der Höhe BCBC (die man entsprechend verschoben auch im Dreieck ABEABE erhält). Analoges gilt für die Dreiecke BDHBDH und BCHBCH die in der Seite BHBH und der Höhe BDBD übereinstimmen. Es bleibt zu zeigen, dass die Dreiecke ABEABE und BCHBCH kongruent sind. Es ist:
  • ∣BH∣=∣AB∣=c|BH|=|AB|=c (Hypotenuse)
  • ∣BC∣=∣BE∣=a|BC|=|BE|=a
  • ∠ABE=∠HBC=90°+β\angle ABE=\angle HBC=90°+\beta
Die Dreiecke stimmen in zwei Seiten und dem eingeschlossenen Winkel überein und sind daher kongruent. Daher gilt a2=pca^2=pc
Ebenso kann b2=qcb^2=qc gezeigt werden.

Beweis mittels Höhensatz und Satz des Pythagoras

Zum Beweis benutzen wir den Höhensatz und den Satz des Pythagoras.
Nach dem Höhensatz gilt: h2=pqh^2=pq; also p2+h2=p2+pqp^2+h^2=p^2+pq. Für die linke Seite der Gleichung wenden wir den Satz des Pythagoras im Dreieck ΔBCD\Delta BCD an (p2+h2=a2p^2+h^2=a^2) und erhalten a2=p2+pq=p(p+q)a^2=p^2+pq=p(p+q). Es ist p+q=cp+q=c und damit gilt: a2=pca^2=pc.
Die zweite Behauptung kann analog bewiesen werden, indem man den Satz des Pythagoras im Dreieck ΔADC\Delta ADC anwendet. □\qed
 
 

So seltsam es auch klingen mag, die Stärke der Mathematik beruht auf dem Vermeiden jeder unnötigen Annahme und auf ihrer großartigen Einsparung an Denkarbeit.

Ernst Mach

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Spezielle Dreiecke