Höhensatz im rechtwinkligen Dreieck

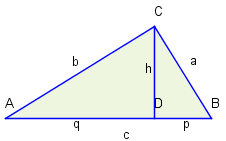
DreieckRwPq.png
In einem rechtwinkligen Dreieck ΔABC\Delta ABC sei cc die Hypotenuse, DD der Fußpunkt der Höhe hh durch CC. Mit pp und qq werden die beiden Hypotenusenabschnitte DB‾\overline {DB} und AD‾\overline {AD} bezeichnet. Es gilt:
h2=pqh^2 = pq
HsBew.png

Beweis

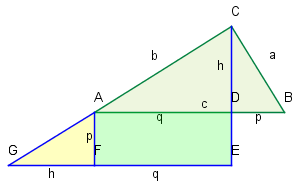
Das große Dreieck △GEC\triangle GEC ergibt sich durch "Ankleben" des Dreiecks △DBC\triangle DBC. Mit den Bezeichnungen in der Grafik erhält man mittels Formel 5504A für seinen Flächeninhalt: A△DBC=12(h+p)⋅(h+q)A_{\triangle DBC}=\dfrac 1 2(h+p)\cdot(h+q). Es gilt A△DBC=pq+A△ABCA_{\triangle DBC}=pq+A_{\triangle ABC}, woraus sich 12(h+p)⋅(h+q)\dfrac 1 2(h+p)\cdot(h+q) =pq+12c⋅h =pq+\dfrac 1 2 c\cdot h=pq+12(p+q)⋅h =pq+\dfrac 1 2(p+q)\cdot h ableitet. Also:(h+p)⋅(h+q)=2pq+(p+q)⋅h(h+p)\cdot(h+q)=2pq+(p+q)\cdot h und h2+ph+qh+pq=2pq+hp+hqh^2+ph+qh+pq=2pq+hp+hq, woraus sich die Behauptung ergibt.
 
 

Beweis durch Ähnlichkeit

Die Dreiecke ΔADC\Delta ADC und ΔBCD\Delta BCD sind ähnlich zueinander. Damit gilt: hq=ph\dfrac{h}{q} = \dfrac{p}{h},
woraus man die Behauptung: h2=pqh^2 = pq erhält. □\qed

Beweis mittels Satz des Pythagoras

Unter Benutzung des Satzes des Pythagoras:
Im Dreieck ΔABC\Delta ABC gilt: c2=a2+b2c^2 = a^2 + b^2; ebenso gelten in den Dreiecken ΔADC\Delta ADC und ΔBCD\Delta BCD: b2=h2+q2b^2 = h^2+q^2 und a2=h2+p2a^2=h^2+p^2.
In die erste Beziehung eingesetzt erhalten wir: c2=h2+p2+h2+q2c^2=h^2+p^2+h^2+q^2 == 2h2+p2+q22h^2+p^2+q^2.
Andererseits ist: c=p+qc=p+q und somit c2=(p+q)2=p2+q2+2pqc^2=(p+q)^2=p^2+q^2+2pq. Setzen wir dies für c2c^2 ein, ergibt sich: p2+q2+2pq=2h2+p2+q2p^2+q^2+2pq=2h^2+p^2+q^2 und damit 2pq=2h22pq=2h^2. Nach der Division durch 2 erhalten wir die Behauptung: h2=pqh^2 = pq. □\qed
HKat.png

Beweis mittels Kathetensatz

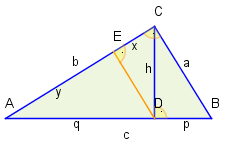
Im Dreieck ABCABC gilt nach Kathetensatz b2=qcb^2=qc =q(p+q)=pq+q2 =q(p+q)=pq+q^2. Im Dreieck ADCADC sei x=∣CE∣x=|CE| und y=∣AE∣y=|AE|. Benutzt man im Dreieck ADCADC den Kathetensatz, so gilt q2=byq^2=by und h2=bxh^2=bx =b(b−y)=b(b-y) =b2−by=b^2-by =b2−q2=b^2-q^2 =pq+q2−q2=pq=pq+q^2-q^2=pq. □\qed
DreieckRwPq.png

Umkehrung

Gilt für ein Dreieck ABCABC mit den nebenstehenden Bezeichnungen h2=pqh^2=pq, so ist das Dreieck rechtwinklig mit dem rechten Winkel bei CC.

Beweis

Aus h2=pqh^2=pq folgt h:p=q:hh:p=q:h und da ∠ADC=∠CDB\angle ADC=\angle CDB, sind die Dreiecke ADCADC und CDBCDB ähnlich. Dann stimmen auch die anderen Winkel überein ∠CAD=∠BCD\angle CAD=\angle BCD und ∠DCA=∠DBC\angle DCA=\angle DBC. Es ist ∠DCA+∠BCD\angle DCA+\angle BCD=∠DCA+∠CAD=90° =\angle DCA+\angle CAD=90° und Dreieck ABCABC ist rechtwinklig. □\qed

Die Mathematik muß man schon deswegen studieren, weil sie die Gedanken ordnet.

M. W. Lomonossow

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Spezielle Dreiecke