Das gleichseitige Dreieck

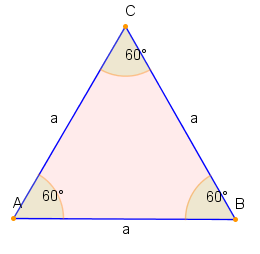
GlSeit.png
Bei einem gleichseitigen Dreieck sind alle drei Seiten gleich lang und daher auch alle drei Innenwinkel gleich groß (60°). Aus diesem Grund gehört das gleichseitige Dreieck auch zu den regelmäßigen Polygonen.
Das gleichseitige Dreieck zählt zu den spitzwinkligen Dreiecken, weil alle drei Winkel kleiner als 90° sind und außerdem ist das gleichseitige Dreieck auch ein gleichschenkliges Dreieck.
Alle gleichseitigen Dreiecke sind zueinander ähnlich, da sie ja stets in den drei gleich großen Winkeln übereinstimmen.
Mittelsenkrechte, Winkelhalbierende, Seitenhalbierende und Höhe zu einer Seite fallen bei einem gleichseitigen Dreieck jeweils zusammen. Entsprechendes gilt für den Umkreismittelpunkt, den Inkreismittelpunkt, den Schwerpunkt und den Höhenschnittpunkt des gleichseitigen Dreiecks.
 
 

Formeln

Umfang

u=3⋅au=3\cdot a

Höhe

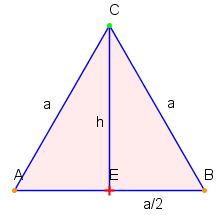
Glsh.png

Flächeninhalt

A=34 a2A = \dfrac{\sqrt{3}}{4} \, a^{2}
Nach der Flächenformel gilt A=12ahA=\dfrac 1 2 a h=12⋅32 a=34 a2 =\dfrac 1 2 \cdot \dfrac{\sqrt{3}}{2} \, a=\dfrac{\sqrt{3}}{4} \, a^{2}.

Formel C94C (Umkreisradius)

r=33 a=a3r = \dfrac{\sqrt{3}}{3} \, a=\dfrac{a}{\sqrt{3}}
Nach Satz 5515F gilt r=a2sin⁡αr=\dfrac a {2\sin\alpha} =a2sin⁡60°=\dfrac a {2\sin 60°} =a2⋅23=\dfrac a 2 \cdot \dfrac 2 {\sqrt 3} (Tabelle 7CGF)

Formel 91NB (Inkreisradius)

ρ=36 a\rho = \dfrac{\sqrt{3}}{6} \, a. Wegen h=32 ah = \dfrac{\sqrt{3}}{2} \, a gilt außerdem h=3ρh=3\rho
Nach Satz 5515J ist ρ=(s−a)(s−b)(s−c)s\rho=\sqrt{ \dfrac {(s-a)(s-b)(s-c)}{s}} mit s=a+b+c2=32as=\dfrac{a+b+c}2=\dfrac 3 2 a. Also ρ=12a⋅12a⋅12a32a\rho =\sqrt{\dfrac {\dfrac 1 2 a\cdot\dfrac 1 2 a\cdot\dfrac 1 2 a }{\dfrac 3 2 a}} =112a2=\sqrt{\dfrac 1 {12} a^2} =36 a= \dfrac{\sqrt{3}}{6} \, a.

Viviani.png
Der folgende Satz geht auf den italienischen Mathematiker Vincenzo Viviani (1622 - 1703) zurück.

Satz 91NA (Satz von Viviani)

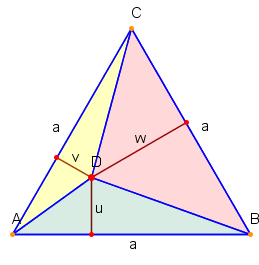
In einen gleichseitigen Dreieck gilt: ist DD ein beliebiger Punkt im Inneren, so ist die Summe der Abstände dieses Punktes von den Seiten konstant und gleich der Länge der Höhe hh.
u+v+w=h=3ρ u+v+w = h = 3\rho
Dabei bezeichnet hh die Höhe des Dreiecks und ρ\rho den Inkreisradius.

Beweis

h=3ρh = 3\rho gilt nach Formel 91NB. Der Beweis wird über eine Flächenzerlegung geführt.
Für die Fläche ADA_D des gleichseitigen Dreiecks ABCABC gilt AD=ah2A_D=\dfrac{ah}2, wobei a=AB‾=BC‾=CA‾a=\overline{AB}=\overline{BC}=\overline{CA} die Grundseite und h h\, die Höhe ist.
In den farbig markierten Dreiecken sind uu, vv und ww gerade die Höhen und für die Flächen gilt: A△ABD=au2A_{\triangle ABD}=\dfrac{au}2, A△CDB=aw2A_{\triangle CDB}=\dfrac{aw}2 und A△ADC=av2A_{\triangle ADC}=\dfrac{av}2. Damit ist
AD=ah2=au2+av2+aw2A_D=\dfrac{ah}2=\dfrac{au}2+\dfrac{av}2+\dfrac{aw}2
Damit folgt die Behauptung h=u+v+wh = u+v+w . □\qed

Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck