Stirling-Formel

Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Sie ist benannt nach dem Mathematiker James Stirling.
Stirlingsche.png
Die Stirling-Formel in ihrer einfachsten Form ist eine Näherungsformel
n!≈2πn (ne)n n! \approx \sqrt{2 \pi n} \, \braceNT{\dfrac{n}{\mathrm e}}^{n}\,
(Zu den einzelnen Elementen dieser Formel siehe Quadratwurzel, π, e.)
Genauer gilt:
1≤n!2πn⋅(ne)n≤e1/(12n)<1+111n1\leq\dfrac{n!}{\sqrt{2\pi n}\cdot(\dfrac n{\mathrm e})^n}\leq\mathrm e^{1/(12n)}<1+\dfrac1{11n}
Insbesondere ist der Grenzwert des Bruches für n→∞n\to\infty gleich 1.
Die Stirling-Reihenentwicklung lautet:
ln⁡(n!)=nln⁡(n)−n+(12)ln⁡(2πn)+(112n)−(1360n3)+(11260n5)−(11680n7)+⋯ \ln (n!)=n\ln (n) - n + \over{1}{2}\ln(2\pi n) +\over{1}{12n} -\over{1}{360n^3} +\over{1}{1260n^5} -\over{1}{1680n^7} +\cdots
Als Näherung betrachtet man lediglich eine endliche Zahl von Gliedern. Der Fehler liegt in der Größenordnung des ersten vernachlässigten Gliedes. Beispiel: bricht man nach dem dritten Glied ab, ist der absolute Fehler kleiner als 112n\dfrac1{12n}.
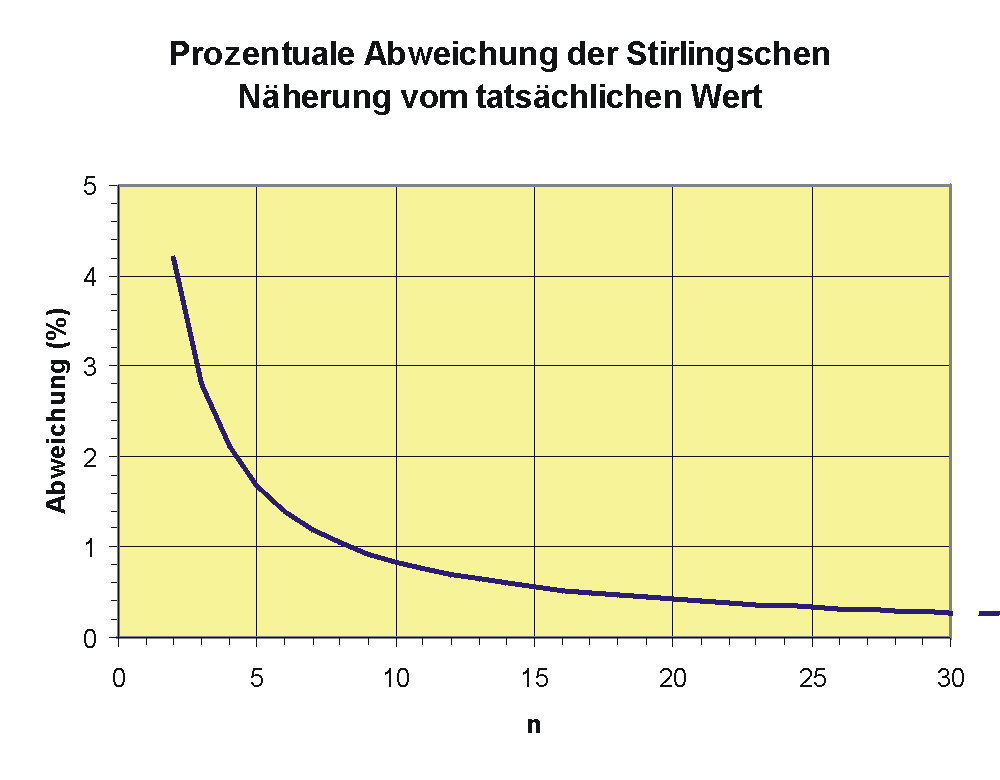
Für n>1000n>1000 genügen zwei Glieder, um den relativen Fehler kleiner als 1 % zu halten:
ln⁡(n!)≈nln⁡(n)−n\ln (n!) \approx n \ln (n) - n
Für sehr große n, n>10440^{44}, reduziert sie sich zu (relativer Fehler < 1 %):
ln⁡(n!)≈n⋅ln⁡(n)\ln (n!) \approx n \cdot \ln (n) .
Beispielsweise folgt daraus, dass die Zahl der Ziffern von 10100!10^{100}! in Dezimaldarstellung bis auf 1 % Genauigkeit gleich 1010210^{102} ist.

Anwendungen

Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Insbesondere bei der Berechnung der Information einer Nachricht und bei der Berechnung der Entropie eines statistischen Ensembles von Subsystemen ergeben sich mit der Stirling-Formel starke Vereinfachungen.
Beispiel: Gegeben sei ein System mit NN verschiedenen Subsystemen, von denen jedes mm verschiedene Zustände annehmen kann. Ferner sei bekannt, dass der Zustand ii mit der Wahrscheinlichkeit ωi\omega_i gemessen wird. Damit müssen sich NiN_i Subsysteme im Zustand ii befinden und es gilt Ni/N=ωiN_i/N=\omega_i. Die Zahl der möglichen Verteilungen eines so beschriebenen Systems beträgt dann
N!/(N1! N2! … Nm!)N!/(N_1! \, N_2! \, \ldots \, N_m!)
und für dessen Entropie σ\sigma gilt
σ=ln⁡(N!)−ln⁡(N1!)−…−ln⁡(Nm!) \sigma=\ln(N!)-\ln(N_1!)-\ldots-\ln(N_m!)\,
Mittels der Stirling-Formel kann man nun bis auf Fehler der Ordnung O(ln⁡(N))O(\ln(N)) diese Formel vereinfachen zu
σ \sigma \, =N(ln⁡N−1)−N1(ln⁡N1−1)−…−Nm(ln⁡Nm−1)=N (\ln N - 1) - N_1 (\ln N_1 - 1) - \ldots - N_m (\ln N_m - 1)
=Nln⁡N−N1ln⁡N1−…−Nmln⁡Nm=N \ln N - N_1 \ln N_1 - \ldots - N_m \ln N_m
=(N1+…+Nm)ln⁡N−N1ln⁡N1−…−Nmln⁡Nm=(N_1 + \ldots + N_m) \ln N - N_1 \ln N_1 - \ldots - N_m \ln N_m
=−N1ln⁡(N1/N)−…−Nmln⁡(Nm/N)=- N_1 \ln (N_1/N) - \ldots - N_m \ln (N_m/N)
=−N∑i=1m(ωiln⁡ωi)=- N \sum\limits_{i=1}^m (\omega_i \ln \omega_i)
Damit ergibt sich für die Entropie jedes der NN Subsysteme die bekannte Formel
σ=−∑i=1mωiln⁡(ωi)\sigma=-\sum\limits_{i=1}^m \omega_i\ln(\omega_i)
In ähnlicher Weise erhält man (bis auf einen konstanten Vorfaktor) für den Informationsgehalt eines ebenso definierten Systems die Formel
I=−∑i=1mωilog⁡2(ωi)I=-\sum\limits_{i=1}^m \omega_i\log_2{(\omega_i)}

Siehe auch

Literatur

 
 

An Archimedes wird man sich erinnern, wenn Aischylos vergessen ist - weil zwar die Sprachen sterben, nicht aber die mathematischen Ideen.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Stirling-Formel aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Induktive Definitionen