Kreisringe
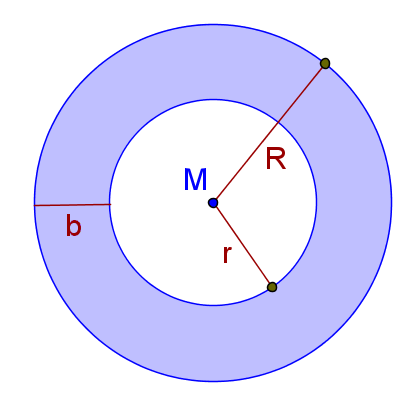
Seien zwei Kreise mit dem gleichen Mittelpunkt , aber unterschiedlichen Radien und mit gegeben. Ein Kreisring ist dann die Fläche zwischen diesen beiden konzentrischen Kreisen.
Die Größe bezeichnet die Ringbreite.
Der Flächeninhalt des Kreisringes ergibt sich als Differenz der beiden Kreisflächen mit:
- .
wobei die Kreiszahl ist.
Mit erhält man: . Gilt , so ist .
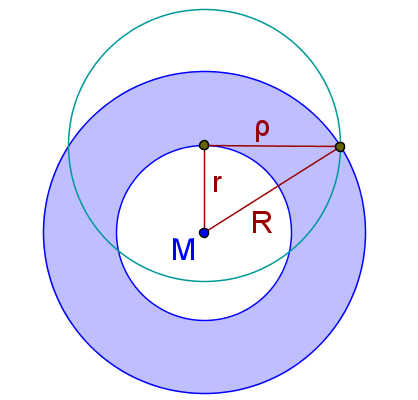
Gleichgroßer Kreis
Sei nun der Radius eines Kreises mit dem gleichen Flächeninhalt wie der Kreisring, es gilt dann , also und . Dies ist eine typische Gleichung, wie sie sich aus dem Satz des Pythagoras ergibt. In der nebenstehenden Abbildung finden wir das rechtwinklige Dreieck und sehen, dass wir den Radius gewinnen können, indem wir eine Tangente an den inneren Kreis zeichnen. Die Verbindungsstrecke zwischen [!Berührungspunkt] der Tangente und dem äußeren Kreis ergibt genau den Radius des gesuchten Kreises.
Das Buch der Natur ist mit mathematischen Symbolen geschrieben.
Galileo Galilei
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе