Approximation des Kreises durch regelmäßige 2n-Ecke

Wir wollen Flächeninhalt und Umfang durch das Einbeschreiben von regelmäßigen $2^n$-Ecken annähern. Beginnen wir mit einem Quadrat.

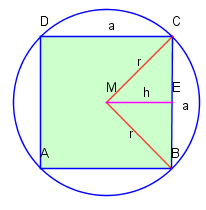
Die Situation mit einem einbeschriebenen Quadrat zeigt die Abbildung. Ist $r$ der Radius des Kreises und $a$ die Seitenlänge des Quadrates, kann man wegen $\angle CMB=90°$ unter Benutzung des Satzes des Pythagoras ableiten: $2r^2=a^2$.

Damit ergibt sich für den Flächeninhalt $A_Q$ und Umfang $u_Q$ des Quadrates:

$A_Q=2r^2$

$u_Q=4a=4\sqrt 2 r$.

Durch Vergleich mit dem Umfang des Kreises, könnten wir für $\pi$ den Näherungswert $\pi\approx 2\sqrt 2\approx 2,828$ gewinnen.

Wenn dem Kreis im Allgemeinen ein regelmäßiges $2^n$-Eck einbeschrieben ist, dessen Seitenlängen $a_n$ sei, können wir uns das $2^n$-Eck in $2^n$ kongruente Teildreiecke zerlegt vorstellen. Beim Viereck ist $\Delta BCM$ ein solches Dreieck. Der Flächeninhalt dieses Dreiecks ist $A_D=\dfrac 1 2 \cdot \dfrac a 2 h= \dfrac {ah} 4$. Im allgemeinen Fall (wenn $h_n$ die Höhe im entsprechenden Teildreieck des $2^n$-Ecks ist) ergibt sich $A_D= \dfrac {a_nh_n} 2$. Da das $2^n$-Eck in $2^n$-Teildreiecke zerlegt wird, ergibt sich $A_n=2^n\cdot \dfrac {a_nh_n} 2= 2^{n-1}\cdot a_nh_n$.

Den Umfang erhält man relativ einfach mit $u_n=2^n\cdot a_n$.

Für das Quadrat hatten wir $a=a_2=\sqrt 2 r$ und $h=h_2=\dfrac a 2= \dfrac 1 2\sqrt 2 r$ ergibt sich unmittelbar aus der Gleichschenkligkeit des Dreiecks $\triangle ECM$. Man überzeugt sich leicht, das man durch Einsetzen ($n=2$ für das Quadrat) wieder zu dem oben angegebenen Ergebnis kommt.

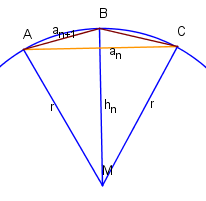
Bleibt die Frage, wie man $a_n$ und $h_n$ allgemein ausrechnet. Dieses Problem werden wir durch Angabe einer Rekursionsgleichung lösen.

In der Abbildung sei $\triangle AMC$ ein Teildreieck im $2^n$-Eck. Dann können wir $h_n$ sofort ausrechnen. Es gilt nach dem Satz des Pythagoras ${h_n}^2+{\dfrac {a_n} 2}^2 =r^2$. Also:

Wenn wir jetzt vom $2^n$-Eck zum $2^{n+1}$-Eck übergehen können wir aus nebenstehender Abbildung die folgende Beziehung ablesen:

Die folgende Tabelle fasst die Ergebnisse für die ersten n zusammen.

Die höheren $h_n$ braucht man nicht wirklich. Man kann nämlich zeigen: $A_{n+1}=u_n r/2$.