Das isoperimetrisches Problem

Das isoperimetrische Problem beschäftigt sich mit der Frage, welche ebene Figur bei vorgehenen Umfang $u$ die größte Fläche $A$ umfasst. In der Ebene ist die Lösung ein Kreis.

Für ebene Figuren gilt die Gleichheit gilt nur für den Kreis.

Die Ungleichung (1) heißt isoperimetrische Ungleichung und wird oft in der Form geschrieben.

Wir folgen hier einem Beweis von Jakob Steiner und setzen die Existenz einer Lösung voraus.

i) Die Gleichheit gilt für einen Kreis Wegen $A=\pi r^2$ und $u=2\pi r$ sieht man sofern, dass in (1) die Gleichheit gilt.

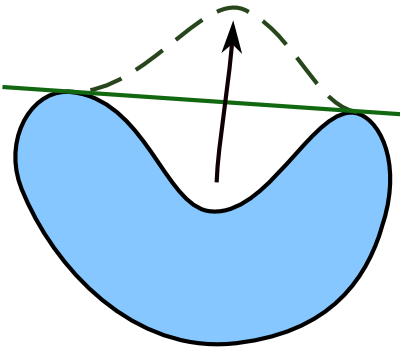
ii) Die gesuchte Figur muss konvex sein.

Denn: wäre die Figur nicht konvex, gäbe es mindestens eine Einbuchtung (vgl. nebenstehende [!Abbildung]) und wir könnten einen Teil der Umrandung durch Spiegelung nach außen stülpen. Die neu enstehende Figur hätte den gleichen Umfang, aber einen größeren Flächeninhalt. Da wir dies mit allen Einbuchtungen machen können, erhalten wir im Ergebnis eine konvexe Figur, mit dem gleichen Umfang, aber größeren Flächeninhalt.

iii) Halbierungsansatz Wir wählen auf dem Umfang unserer (nach i) konvexen) Figur zwei Punkte $A$ und $B$ so, dass der durchlaufene Umfang von $A$ nach $B$ genauso groß ist, wie der von $B$ nach $A$. Die Verbindungsstrecke $\ovl{AB}$ muss unsere Figur in zwei flächengleiche Teilfiguren zerlegen.

Denn angenommen wir haben zwei Punkte $A$ und $B$ auf dem Umfang, deren Verbindungsstrecke den Flächeninhalt unserer Figur nicht halbiert. Dann muss der Flächeninhalt einer Teilfigur größer sein als der der anderen. Wenn wir nun die größere Teilfigur an der Strecke $\ovl{AB}$ spiegeln, erhalten wir eine Figur mit größerem Flächeninhalt bei gleichem Umfang.

iv) Wir zeigen jetzt, dass unter allen Figuren über einer Basisstrecke $\ovl{AB}$, der Halbkreis den größten Flächeninhalt bei vorgegeben Umfang hat.

Man betrachte zu einem beliebigen Punkt $C$ der Kurve das Dreieck $ABC$. Dieser Punkte $C$ teilt die Fläche $A$ zwischen der Kurve und der Stecke $\ovl{AB}$ in drei Teilflächen auf: die Fläche $A_1$ des Dreiecks $ABC$ und die Flächen $A_2$ zwischen der Kurve und der Dreiecksseite $\ovl{AC}$ und $A_3$ zwischen der Kurve und der Seite $\ovl{CB}$.

Wir variieren die Winkel $\gamma$ bei $C$, lassen jedoch die Strecken $b=\ovl{AC}$ und $a=\ovl{CB}$ (und damit den Umfang der Kurve) unverändert. Mit Formel 5518B gilt $A_1=ab\cdot\sin\gamma$. Da der Sinus sein Maximum bei $90°$ annimmt, wird $A_1$ maximal, wenn das Dreieck $ABC$ rechtwinklig ist.

Die gesuchte Fläche hat also jeweils rechte Winkel in beliebigen Punkten $C$ der Kurve und ist somit nach dem Satz des Thales ein Halbkreis. $\qed$