Zentri-Peripherie-Winkelsatz

Peripheriwinkel.png
Zwischen Zentriwinkeln und Peripheriewinkeln am Kreis besteht ein einfacher Zusammenhang:

Satz 166P (Zentri-Peripherie-Winkelsatz)

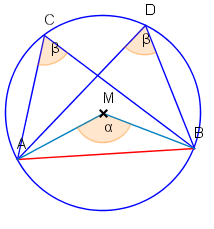
Jeder Zentriwinkel (in der gleichen Halbebene) über einem Kreisbogen ist doppelt so groß wie der dazugehörige Peripheriewinkel.
In der Abbildung: β=α2\beta=\dfrac\alpha 2.

Beweis

Zum Beweis führen wir eine Fallunterscheidung durch. Für den Mittelpunkt des Kreises gibt es drei Möglichkeiten im Verhältnis zum Dreieck mit dem Peripheriwinkel:
  1. Er liegt auf einer Seite
  2. Er liegt innerhalb des Dreiecks
  3. Er liegt außerhalb des Dreiecks
Wir beweisen den Satz für jeden dieser Fälle einzeln
Fall 1
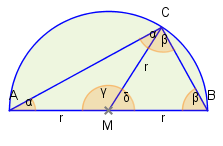
thalesb1.png
In der Abbildung ist dieser Fall veranschaulicht. Winkel ∠AMB=γ+δ=180°\angle AMB = \gamma+\delta=180° ist der Zentriwinkel. Winkel ∠ACB=α+β\angle ACB = \alpha +\beta ist der Peripheriwinkel.
Wie müssen zeigen, dass dieser Winkel eine Größe von 90° hat. Damit hätten wir nicht nur diesen Fall abgehandelt, sondern auch gleich den Satz des Thales bewiesen.
Wir führen den Beweis über Winkelgrößen.
Seien AA und BB Punkte auf dem Durchmesser eines Kreises mit dem Radius rr. CC liege auf dem Kreis.
Wir ziehen die Verbindungsstrecke CM‾\overline{CM} und erhalten zwei Teildreiecke ΔAMC\Delta AMC und ΔBCM\Delta BCM.
Die Bezeichnung der Winkel entnehme man der Zeichnung. Dabei ist klar, dass die jeweils mit α\alpha und β\beta bezeichneten Winkel gleich groß sind, da sie jeweils einer gleichlangen Seite (der Länge rr) gegenüberliegen. Damit können wir ausgehend vom Winkel α\alpha schrittweise die anderen Winkel berechnen.
Nach dem Innenwinkelsatz gilt im Dreieck ΔAMC\Delta AMC: 2α+γ=180°2\alpha+\gamma=180°, also γ=180°−2α\gamma=180°-2\alpha. δ\delta und γ\gamma ergänzen sich zu 180° also ist
δ=2α\delta=2\alpha.
Damit ist der Satz auch gezeigt wenn B‾C\overline BC die Basisstrecke ist und δ\delta der Zentriwinkel und α\alpha der Peripheriwinkel.
Im Dreieck ΔBCM\Delta BCM gilt somit 2α+2β=180°2\alpha+2\beta=180° also β=90°−α\beta=90°-\alpha. Damit ist aber, unabhängig vom konkreten Wert von α\alpha, die Summe α+β\alpha+\beta immer 90° groß.
Fall 2
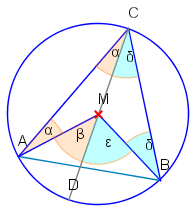
PeripheriwinkelB1.png
Dieser Fall ist in nebenstehender Abbildung veranschaulicht. Durch eine ähnliche Schlußweise wie in Fall 1 erhalten wir: Die beiden α\alpha-Winkel sind wirklich gleich groß, da sie gleichlangen Seiten gegenüberliegen (Länge ist der Radius).
Es gilt ∠AMC+2α=180°\angle AMC +2\alpha = 180° und ∠AMC+β=180°\angle AMC + \beta=180° ergibt sich β=2α\beta=2\alpha.
Analog kann man erschließen, dass ϵ=2δ\epsilon=2\delta ist.
Bildet man die Summe von beiden Beziehungen erhält man die Behauptung.
Fall 3In diesem Fall wird die Rechnerei etwas aufwendiger, wodurch wir uns jedoch nicht abschrecken lassen.
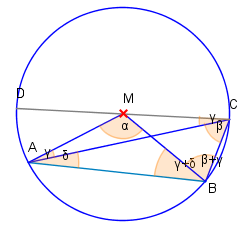
Peripheriewinkelb2.png
Wir bemerken zuerst, dass A‾M=B‾M=C‾M\overline AM =\overline BM =\overline CM ist. Aus der Gleichschenkligkeit der entsprechenden Dreiecke ergibt sich dann die Gleichheit der entsprechenden Winkel. Im Dreieck ΔABM\Delta ABM gilt: ∠BAM=∠MBA=γ+δ\angle BAM = \angle MBA=\gamma+\delta; im Dreieck ΔBCM\Delta BCM gilt: ∠MBC=∠BCM=β+γ\angle MBC=\angle BCM = \beta+\gamma.
Wir benutzen wieder den Innenwinkelsatz und stellen fest, dass im Dreieck ΔABM\Delta ABM gilt: α+2γ+2δ=180°\alpha + 2\gamma +2\delta=180°; ebenso gilt im Dreieck ΔABC\Delta ABC: δ+(γ+δ+β+γ)+β\delta+(\gamma+\delta+\beta+\gamma)+\beta == 2γ+2δ+2β=180°2\gamma+2\delta+2\beta=180°. Somit erhalten wir: 2γ+2δ=180°−2β2\gamma+2\delta=180°-2\beta
Setzen wir dies in die erste Gleichung ein gilt: α+180°−2β=180°\alpha +180°-2\beta=180°, also die Behauptung α=2β\alpha=2\beta.
Damit hätten wir den Satz in Gänze bewiesen. □\qed
 
 

Die Mathematik ist eine Art Spielzeug, welches die Natur uns zuwarf zum Troste und zur Unterhaltung in der Finsternis.

Jean-Baptist le Rond d'Alembert

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Der Kreis