Sätze über Höhen im Dreieck

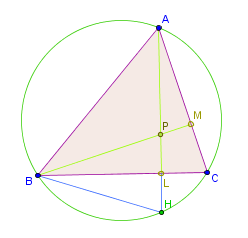
hsuk.png

Satz A7RF (Höhenschnittpunkt und Umkreis)

Die Gerade durch AA und den Höhenfußpunkt LL schneide den Umkreis in HH. Dann gilt ∣PL‾∣=∣LH‾∣|\ovl{PL}|=|\ovl{LH}|, wobei PP der Höhenschnittpunkt ist.
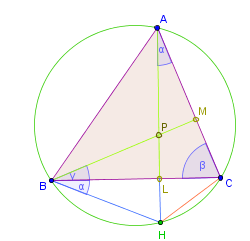
hsuk1.png

Beweis

Nach dem Peripheriewinkelsatz über die Sehne HC‾\ovl{HC} sind die im Bild mit α\alpha bezeichneten Winkel gleich groß. Im Dreieck ΔALC\Delta ALC gilt α+β=90°\alpha+\beta=90° und im Dreieck ΔBCM\Delta BCM gilt γ+β=90°\gamma+\beta=90°, also α=γ\alpha=\gamma. Die Dreiecke ΔBLP\Delta BLP und ΔBHL\Delta BHL stimmen damit in 2 Winkeln (α=γ\alpha=\gamma und einem rechten) und einer Seite BL‾\ovl{BL} überein, sind damit kongruent, also ∣PL‾∣=∣LH‾∣|\ovl{PL}|=|\ovl{LH}|. □\qed
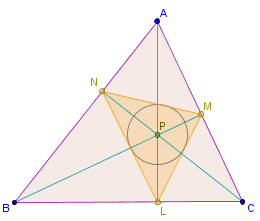
auf1.png

Satz A7TD (Inkreis des Höhenfußpunktdreiecks)

In einem spitzwinkligen Dreieck ΔABC\Delta ABC bilden man ein Dreieck ΔLMN\Delta LMN, indem man die Höhenfußpunkte verbindet. Der Inkreismittelpunkt von ΔLMN\Delta LMN ist der Höhenschnittpunkt von ΔABC\Delta ABC.
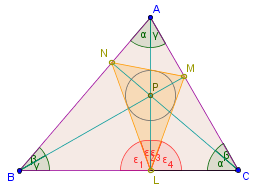
auf1a.png

Beweis

Wir zeigen zuerst, dass die mit α\alpha, β\beta und γ\gamma bezeichneten Winkel tatsächlich gleich groß sind. Dreieck △ABL\triangle ABL und △CNB\triangle CNB sind ähnlich, denn sie stimmen in einem rechten Winkel und dem Winkel bei BB überein, daher α=∠BAL=∠BCN\alpha=\angle BAL=\angle BCN. Analog schließt man für die anderen Winkel. Außerdem gilt, da das Dreieck △ALC\triangle ALC rechtwinklig ist
α+β+γ=90°\alpha+\beta+\gamma=90°(1)
Betrachten wir jetzt die am Scheitel LL liegenden Winkel ϵ1\epsilon_1 ... ϵ4\epsilon_4. Da AL‾\ovl {AL} eine Höhe ist, gilt
ϵ1+ϵ2=ϵ3+ϵ4=90°\epsilon_1+\epsilon_2=\epsilon_3+\epsilon_4=90°(2)
, Wenden wir die Umkehrung des Peripheriewinkelsatzes auf die Sehne LM‾\ovl{LM} an, so ergibt sich, dass ABLMABLM ein Sehnenviereck ist und daher gilt ϵ1+ϵ2+ϵ3+α+γ=180°\epsilon_1+\epsilon_2+\epsilon_3+\alpha+\gamma=180°, also mit (1)
ϵ1+ϵ2+ϵ3=90°+β\epsilon_1+\epsilon_2+\epsilon_3=90°+\beta(3)
.
Ein analoger Schluss mit der Sehne LN‾\ovl {LN } ergibt.
ϵ2+ϵ3+ϵ4=90°+β\epsilon_2+\epsilon_3+\epsilon_4=90°+\beta(4)
.
Subtrahiert man (3) und (4), ergibt sich ϵ1=ϵ4\epsilon_1=\epsilon_4, und mit (2) ϵ2=ϵ3\epsilon_2=\epsilon_3. Damit ist die Höhe AL‾\ovl {AL } Winkelhalbierende des Winkels ∠NLM\angle NLM. Ähnliche Schlüssel für die anderen Winkel zeigt, dass PP der Schnittpunkt der Winkelhalbierenden des Dreiecks ΔLMN\Delta LMN ist und nach Satz 5515H Mittelpunkt des Inkreises.
Aus (2) und (3) können wir auch sofort ϵ2=β\epsilon_2=\beta schließen, womit der Innenwinkel bei LL 2β=2⋅(90°−α−γ)2\beta=2\cdot (90°-\alpha-\gamma) ist, also dem Doppelten des Komplements des gegenüberliegenden Winkels des Ausgangsdreiecks entspricht. □\qed
 
 

Die beste von allen Sprachen der Welt ist eine künstliche Sprache, eine ziemlich gedrängte Sprache, die Sprache der Mathematik.

N. I. Lobatschewski

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Besondere Linien