Das reguläre Sechseck

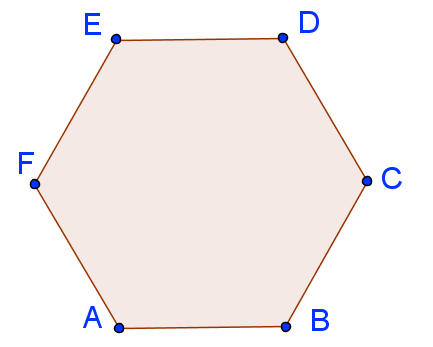
6e.png
Ein reguläres Polygon mit sechs Eckpunkten heißt reguläres Sechseck oder auch Hexagon. Ist keine Verwechslung mit nicht regulären Sechsecken zu befürchten spricht man auch einfach vom Sechseck.
6eWi.png

Formeln

Innenwinkel

Wenden wir Satz C7PF über die Innenwinkelsumme in konvexen Polygonen an, so erhalten wir
∑α=(n−2)⋅180∘ \sum\limits {\alpha =}(n - 2) \cdot 180^\circ =4⋅180∘=720∘= 4 \cdot 180^\circ = 720^\circ.
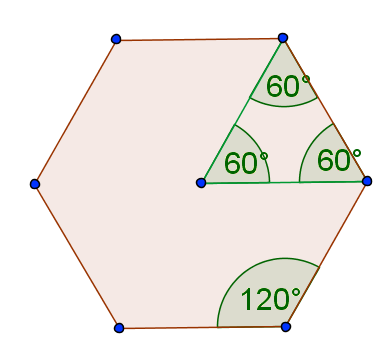
Damit ergibt sich für den Innenwinkel α=720°6\alpha=\dfrac {720°} 6, also:
α=120∘ \alpha = 120^\circ.
Für das in der [!Abbildung] angegebene Dreieck sind damit alle Innenwinkel 60°60° groß. Damit wird ein Sechseck in 6 kongruente gleichseitige Dreiecke zerlegt.
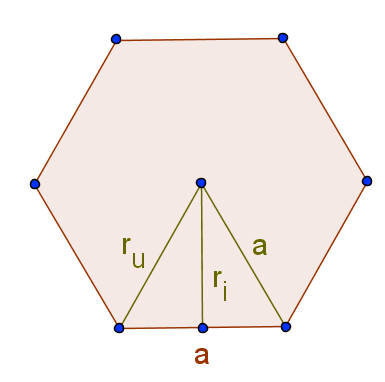
6eUk.png
 
 

Inkreis und Umkreis

Aus den Bezeichnungen für die Höhe des gleichseitigen Dreiecks können wir die Länge des Inkreisradius ableiten:
ri=32a r_i = \dfrac{\sqrt{3}} {2} {a}.
Für die Umkreis gilt einfach:
ru=ar_u=a.

Flächeninhalt

Da ein Sechsecke aus 6 kongruenten gleichseitigen Dreiecken mit der Seitenlänge aa zusammengesetzt ist, ergibt sich die Flächenformel zu:
A=3⋅32a2 A =\dfrac{3\cdot \sqrt 3 }{2} a^2 .
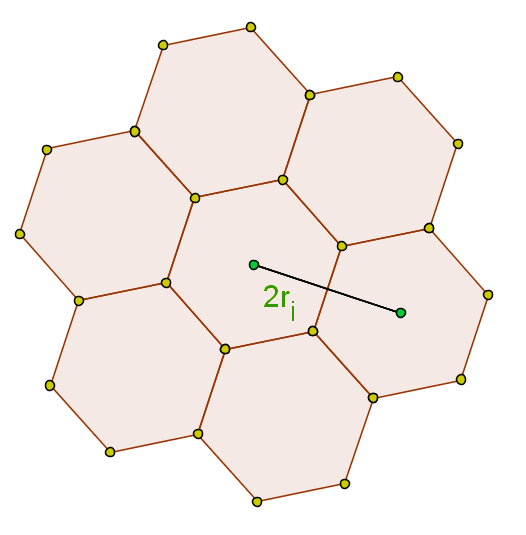
6ePa.png

Parkettierung

Da sich die Innenwinkel von 120°120° von 3 kongruenten - an einer Ecke zusammenstoßenden - Sechsecken zu 360°360° ergänzen, kann man die Ebene mit regelmäßigen Sechsecken ückenlos füllen (parkettieren). Eine derartige Füllung heißt hexagonale Struktur.
Die Mittelpunkte zweier direkt benachbarter Sechsecke haben den Abstand von
2ri=a32 r_i = a \sqrt 3.

Strukturen sind die Waffen der Mathematiker.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie