Rotationsellipsoid

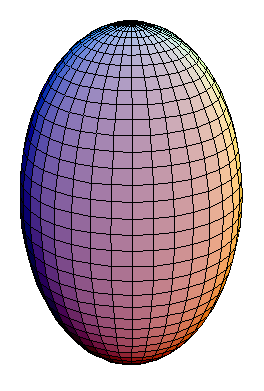
ProlateSpheroid.png
prolates Rotationsellipsoid
Ein Rotationsellipsoid (auf Englisch "spheroid") ist ein Ellipsoid, das durch die Drehung einer Ellipse um eine ihrer Achsen entsteht. Im Gegensatz zu einem allgemeinen Ellipsoid sind zwei Achsen gleich lang. Man unterscheidet dabei je nach Länge der Drehachse das
  • Abgeplattete (oblate) Ellipsoid bei Rotation um die kleine Achse und das
  • Verlängerte (prolate) Ellipsoid bei Rotation um die große Achse.
Ein Beispiel für ein verlängertes Rotationsellipsoid ist die Form des Balles beim Rugby oder American Football.
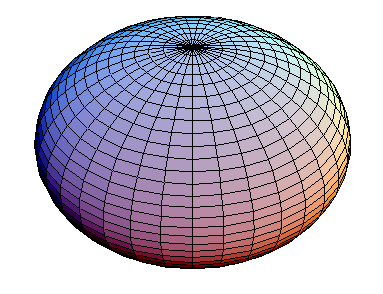
OblateSpheroid.png
Die meisten größeren Himmelskörper sind angenähert abgeplattete Rotationsellipsoide. Sie entstehen durch die Fliehkraft, die bewirkt, dass ein kugelförmiger Körper verformt wird.
Die Oberfläche für das abgeplattete Ellipsoid ist
A=2πa2bb2−a2[ba2b2−a2+arcsin⁡(b2−a2a)]A = \dfrac{2 \pi a^2 b}{\sqrt{b^2-a^2}} \ntxbraceL{\dfrac{b}{a^2}\sqrt{b^2-a^2} + \operatorname{arcsin} \braceNT{\dfrac{\sqrt{b^2-a^2}}{a}}},
die des verlängerten ist
A=2πa2ba2−b2[ba2a2−b2+arcsin⁡(a2−b2a)]A = \dfrac{2 \pi a^2 b}{\sqrt{a^2-b^2}} \ntxbraceL{\dfrac{b}{a^2}\sqrt{a^2-b^2} + \operatorname{arcsin} \braceNT{\dfrac{\sqrt{a^2-b^2}}{a}}}.
Hier ist aa jeweils die Halbachse des Ellipsoids, die zur Rotationsachse parallel ist, bb ist die zur Rotationsachse senkrechte Halbachse des Ellipsoids.
 
 

Wir Mathematiker sind die wahren Dichter, nur müssen wir das, was unsere Phantasie schafft, noch beweisen.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Rotationsellipsoid aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Raum