Paraboloide

Ein Paraboloid ist eine Fläche 2. Ordnung.
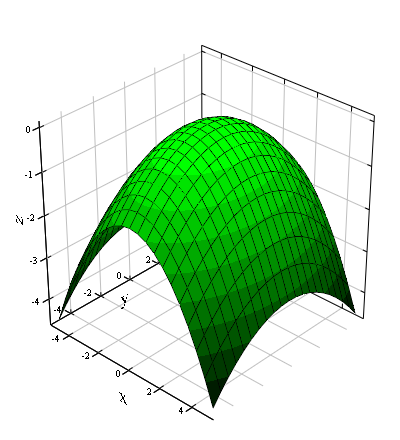
Elliptic_paraboloid.png
elliptisches Paraboloid
Es wird zwischen einem elliptischen und einem hyperbolischen Paraboloiden unterschieden. Das elliptische Paraboloid gleicht - je nach Stärke der Krümmung - einer Schale oder einer Tasse. Das hyperbolische Paraboloid ist eine Sattelfläche.
Die Formel für ein Paraboloid mit der Achse in z-Richtung ist:
  • elliptisches Paraboloid: x2a2+y2b2−z=0\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - z = 0
  • hyperbolisches Paraboloid: x2a2−y2b2−z=0\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} - z = 0
Wird ein Paraboloid von einer Ebene senkrecht zu seiner Achse geschnitten, so ist das Schnittbild eine Ellipse bzw. Hyperbel. Ein Ebenenschitt parallel zur Achse ergibt eine Parabel.
Ein elliptisches Paraboloid mit a=ba=b wird auch als Rotationsparaboloid bezeichnet.

Formeln

Die Formeln gelten für ein Rotationsparaboloid, das von einer zur z-Achse senkrechten Ebene (xy-Ebene) in der Höhe hh abgeschnitten wird. Der Schnittkreis besitzt den Radius rr.
Volumen : V=π2⋅r2⋅hV = \dfrac{\pi}{2} \cdot r^2 \cdot h
Oberfläche (ohne Deckkreisfläche): AO=πr6h2⋅[(r2+4h2)32−r3] A_O = \dfrac{\pi r}{6 h^2} \cdot \ntxbraceL{ \braceNT{ r^2+4 h^2}^{\dfrac{3}{2}} - r^3 }
Höhe des Schwerpunkts: hS=23⋅hh_S = \dfrac{2}{3}\cdot h

Hyperbolisches Paraboloid

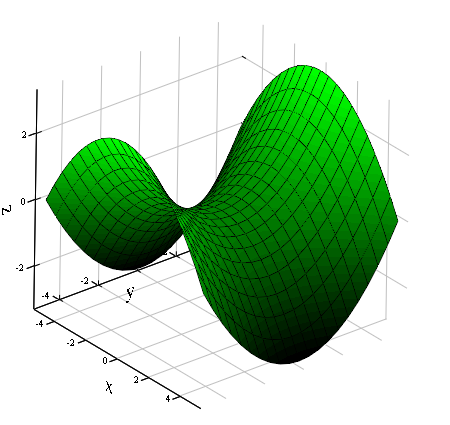
Hyperbolic_paraboloid.png
Hyperbolisches Paraboloid
Das hyperbolische Paraboloid (Sattelfläche) ist mathematisch betrachtet eine Fläche zweiter Ordnung. Das bedeutet, dass jeder Schnitt mit einer Ebene einen Kegelschnitt ergibt. In diesem Fall sind das:
  • bei senkrechten Ebenen: Parabeln
  • bei waagrechten oder beliebig geneigten Ebenen: Hyperbeln
Eine solche Fläche bezeichnet man auch als eine antiklastisch (= gegensinnig) gekrümmte Fläche.
Die Gleichung des hyperbolischen Paraboloids lautet: x2a2−y2b2−2z=0\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} - 2z = 0
Erzeugen kann man die Fläche, indem man eine hängende (nach unten offene) Parabel entlang einer stehenden Parabel, die nach oben offen ist verschiebt. Interessant ist, dass es jedoch auch durch zwei Scharen von Geraden dargestellt werden kann. Das bedeutet, dass das hyperbolische Paraboloid aus geradlinigen Elementen (Seilen, Stahlträgern) konstruiert werden kann.

Siehe auch

 
 

Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Paraboloid;wp:Hyperbolisches Paraboloid aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Raum