Null- und Polstellen rationaler Funktionen

Nullstellen

Die Nullstellen einer rationalen Funktion f(x)=g(x)h(x)f(x)=\dfrac {g(x)} {h(x)} stimmen mit den Nullstellen des Zählerpolynoms g(x)g(x) überein, sofern an diesen Stellen h(x)≠0h(x)\neq 0 gilt. Dies ist immer der Fall, wenn die Funktion in Normalform gegeben war.
 
 
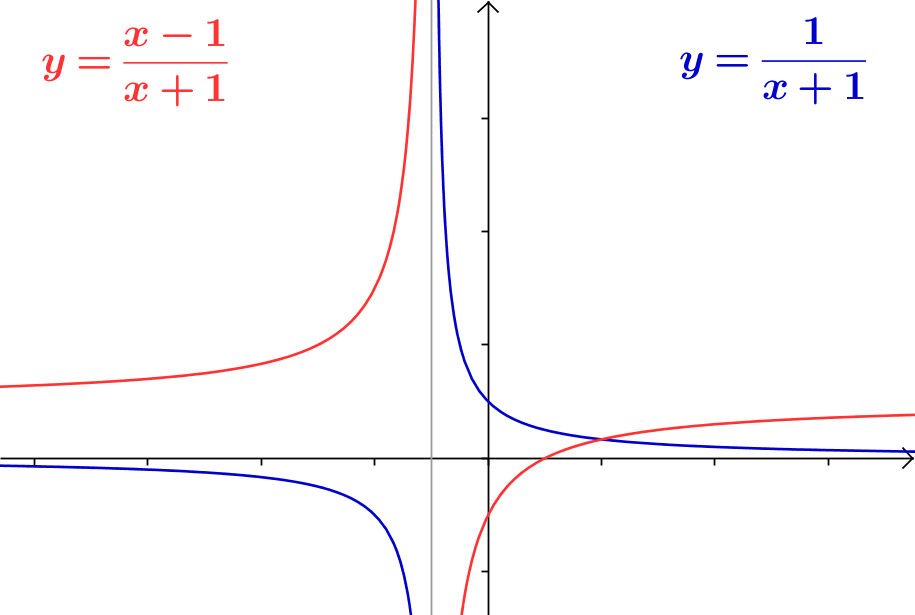
ratfunc2.png

Beispiele

1) f1(x)=x−1x+1f_1(x)=\dfrac {x-1} {x+1} hat die Nullstelle x0=1x_0=1.
2) f2(x)=x−1x2−1f_2(x)=\dfrac {x-1} {x^2 -1} hat an der Stelle x0=1x_0=1 keine Nullstelle, da der Nenner an dieser Stelle 00 ist. Die Normalform dieser rationalen Funktion ist 1x+1\dfrac 1 {x+1}, und besitzt keine Nullstellen.

Polstellen rationaler Funktionen

Sie die rationale Funktion ff der Quotient zweier Polynome gg und hh:
f(x)=g(x)h(x)f(x)=\dfrac {g(x)} {h(x)},
wobei gg und hh verschieden vom Nullpolynom sind. Dann können Polstellen von ff generell nur an den Nullstellen des Nennerpolynoms auftreten. Sei nun x0x_0 eine kk-fache Nullstelle von hh, dann gilt nach dem Fundamentalsatz der Algebra:
h(x)=(x−x0)k⋅S(x)h(x) = (x-x_0)^k \cdot S(x),
dabei ist SS ein Polynom vom Grad n−kn-k und S(x0)≠0S(x_0) \neq 0. Abhängig vom Wert von g(x0)g(x_0) gilt nun:
  • Falls g(x0)≠0g(x_0) \neq 0 gilt, dann ist x0x_0 eine Polstelle der Ordnung kk.
  • Hat g g eine jj-fache Nullstelle in x0x_0, so gilt:
    • falls j<kj<k, so ist x0x_0 Polstelle von ff mit Ordnung k−jk-j;
    • falls j≥kj\geq k, so ist x0x_0 eine stetig behebbare Definitionslücke und somit keine Polstelle.
Rationale Funktionen besitzen höchstens endlich viele Polstellen, da ein Polynom nur endlich viele Nullstellen haben kann und sie können keine anders gearteten Singularitäten besitzen.

Beispiel

xP=−1x_P=-1 ist eine Polstelle für f1(x)=x−1x+1f_1(x)=\dfrac {x-1} {x+1} und f2(x)=1x+1f_2(x)=\dfrac 1 {x+1}.

Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen