Näherungsformeln für Sinus und Kosinus

Eine Anwendung der Taylorformel sind Näherungsformeln, hier vorgestellt für Sinus und Kosinus (wobei das Argument im Bogenmaß angegeben wird).
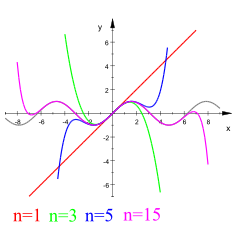
TSin.png
Das 3. Taylorpolynom T3,sin⁡T_{3,\sin} der Sinusfunktion an der Entwicklungsstelle 0 hat diese Gestalt:
sin⁡(x)≈T3,sin⁡(x)=x−x36 \sin(x) \approx T_{3,\sin}(x) = x - \dfrac{x^3}{6}
Liegt xx zwischen −p4\displaystyle{-\frac{{p}}{{4}}} und p4\displaystyle{\frac{{p}}{{4}}}, dann liegt die relative Abweichung ∣(T3,sin⁡(x)−sin⁡(x))/sin⁡(x)∣|(T_{3,\sin}(x)-\sin(x))/\sin(x)| bei unter 0,5%.
Die Abbildungen zeigen die Graphen einiger Taylorpolynome TnT_{n} des Sinus für n=1,3,5,15… n =1, 3, 5, 15\dots und des Cosinus für n=2,4,6,12… n =2,4,6,12\dots.
Das vierte Taylorpolynom T4,cos⁡T_{4,\cos} der Kosinusfunktion an der Entwicklungsstelle 0 hat im Horner-Schema diese Gestalt:
cos⁡(x)≈T4,cos⁡(x)=(x212−1)⋅x22+1 \cos(x) \approx T_{4,\cos}(x) = \left( \dfrac{x^2}{12} - 1 \right) \cdot \dfrac{x^2}{2} + 1
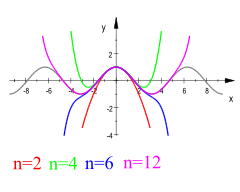
TCos.png
Liegt xx zwischen -p/4 und p/4, dann liegt die relative Abweichung ∣(T4,cos⁡(x)−cos⁡(x))/cos⁡(x)∣|(T_{4,\cos}(x)-\cos(x))/\cos(x)| bei unter 0,05%.
Will man mit diesen Näherungsformeln den Sinus oder Kosinus von anderen xx-Werten berechnen, sollte man die Reduktionsformeln benutzen, um ∣x∣| x | kleiner als p/4 zu machen.
Auch für Tangens und Kotangens kann man diese Formeln nutzen, denn es ist
tan⁡(x) t(x)=T3,sin⁡(x)/T4,cos⁡(x)\tan(x) ~ t(x) = T_{3,\sin}(x) / T_{4,\cos}(x)
mit einer relativen Abweichung von unter 0,5% für ∣x∣<p/4| x | <p/4, und cot⁡(x)∼1/t(x)\cot( x ) \sim 1/t( x ) mit derselben relativen Abweichung. (Dabei ist tt kein Taylorpolynom des Tangens.)
Braucht man eine noch höhere Genauigkeit für seine Näherungsformeln, dann kann man auf höhere Taylorpolynome zurückgreifen, die die Funktionen noch besser approximieren.
 
 

Es gibt keinen Königsweg zur Mathematik.

Euklid

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Taylor-Formel aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Differentialrechnung