Satz von Fermat

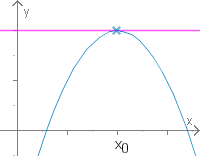
Fermat.png
Die erste Ableitung verschwindet an Stellen, wo die Funktion ein Maximum oder Minimum annimmt. Geometrisch ist dort die Tangente an die Kurve parallel zur x-Achse und hat daher den Anstieg 0.

Satz 15VE (Fermat)

Sei ff eine im abgeschlossenen Intervall [a,b][a,b] stetige Funktion und im offenen Intervall ]a,b[]a,b[ differenzierbar. Nimmt die Funktion in einem Punkt x0∈]a,b[x_0\in]a,b[ ihr Minimum (Maximum) an, so gilt dort f ′(x0)=0f\, '(x_0)=0.

Beweis

Indiekt. Nehme ff in x0x_0 ihr Maximum an und es gelte f ′(x0)≠0f\, '(x_0)\neq 0. Dann ist entweder f ′(x0)>0f\, '(x_0)> 0 oder f ′(x0)<0f\, '(x_0)< 0. Sei f ′(x0)>0f\, '(x_0)> 0. Dann finden wir nach Satz 15VD eine Umgebung um x0x_0 für die
f(x)−f(x0)x−x0>0\dfrac {f(x)-f(x_0)}{x-x_0}>0
gilt. Für x>x0x>x_0 gilt dann f(x)>f(x0)f(x)>f(x_0), im Widerspruch dazu, dass ff in x0x_0 ihr Maximum annahm.
Analog schließt man für f ′(x0)<0f\, '(x_0)< 0, dass es eine Umgebung mit
f(x)−f(x0)x−x0<0\dfrac {f(x)-f(x_0)}{x-x_0}<0
gibt. Hier gilt nun für x<x0x<x_0, dass f(x)>f(x0)f(x)>f(x_0) ist, was zu einem analogen Widerspruch führt.
Der Beweis im Falle des Minimums kann entsprechend geführt werden. □\qed
 
 

Das Buch der Natur ist mit mathematischen Symbolen geschrieben.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Differentialrechnung