Mittelwertsatz der Differentialrechnung

Satz 5227V (Mittelwertsatz)

Sei ff eine im abgeschlossenen Intervall [a,b][a,b] stetige Funktion und im offenen Intervall ]a,b[]a,b[ differenzierbar, dann gibt es ein x0∈]a,b[x_0\in ]a,b[ mit:
f ′(x0)= f(b)−f(a)b−af\, '(x_0)=\, \dfrac {f(b)-f(a)}{b-a}(1)

Andere Formulierung

Sei f:]a,b[→Rf:]a,b[\rightarrow \R auf differenzierbar; x, x+h∈]a,b[x,\, x+h\in ]a,b[. Dann gibt es ein 0<ϑ<10<\vartheta<1, so dass
f(x+h)−f(x)=f′(x+ϑh) h f(x+h)-f(x)=f'(x+\vartheta h)\, h

Geometrische Deutung

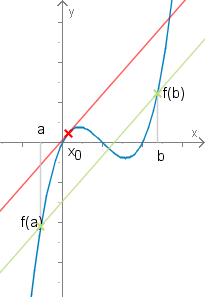
MwDiff.png
Der auf der rechten Seite von (1) stehende Ausdruck entspricht dem Anstieg der Sekante durch die Punkte (a;f(a))(a;f(a)) und (b;f(b))(b;f(b)). Der Satz sagt nun aus, dass es einen Punkt x0∈[a,b]x_0\in[a,b] gibt, so dass der Anstieg der Tangente an die Kurve in diesem Punkt dem Anstieg der Sekante entspricht. Geometrisch ist die Tangente dann also parallel zur Sekante.

Beweis

Wir definieren eine Hilfsfunktion:
g(x):=f(x)−f(b)−f(a)b−a(x−a)g(x):=f(x)-\dfrac{f(b)-f(a)}{b-a}(x-a).
Für diese Funktion gilt: g(a)=f(a)g(a)=f(a) und
g(b)=f(b)−f(b)−f(a)b−a(b−a)=f(a)g(b)=f(b)-\dfrac{f(b)-f(a)}{b-a}(b-a)=f(a).
Damit erfüllt gg alle Voraussetzungen für den Satz von Rolle und es gibt ein x0∈]a,b[x_0\in]a,b[ mit g′(x0)=0g'(x_0)=0. Damit ist aber
f ′(x0)−f(b)−f(a)b−a=0f\, '(x_0)-\dfrac{f(b)-f(a)}{b-a}=0. □\qed

Folgerung 16MC

Sei II ein Intervall und f:I→Rf: I\to \R sei differenzierbar auf II. Dann gilt: ff ist konstant auf II   ⇔  f′=0\;\Leftrightarrow\; f'=0 auf II.

Beweis

"⇒\Rightarrow": klar wegen f ′(c)=0f\, '(c)=0. "⇐\Leftarrow": Seien a,b∈Ia,b\in I und a<ba<b. Nach dem Mittelwertsatz existiert ein ξ∈(a,b)\xi\in (a,b) mit
f(b)−f(a)b−a=f′(ξ)=0\dfrac{f(b)-f(a)}{b-a}=f'(\xi)=0
⇒  f(a)=f(b)  \Rightarrow\; f(a)=f(b)\; ⇒  f\Rightarrow\;f ist konstant, da aa und bb beliebig gewählt. □\qed

Satz 5227W (Verallgemeinerter Mittelwertsatz)

Seien ff und gg in [a,b][a,b] stetige Funktionen und in ]a,b[]a,b[ differenzierbar, gg habe in ]a,b[]a,b[ keine Nullstellen, dann gibt es ein x0∈]a,b[x_0\in ]a,b[ mit
f ′(x0)g′(x0)= f(b)−f(a)g(b)−g(a)\dfrac {f\, '(x_0)}{g'(x_0)}=\, \dfrac {f(b)-f(a)} {g(b)-g(a)}.

Beweis

Wir definieren eine Hilfsfunktion:
h(x):=[f(b)−f(a)]g(x)−[g(b)−g(a)]f(x)h(x):=[f(b)-f(a)]g(x)-[g(b)-g(a)]f(x).
Es gilt
h(a)=[f(b)−f(a)]g(a)−[g(b)−g(a)]f(a)=f(b)g(a)−f(a)g(b)h(a)=[f(b)-f(a)]g(a)-[g(b)-g(a)]f(a)=f(b)g(a)-f(a)g(b)
und
h(b)=[f(b)−f(a)]g(b)−[g(b)−g(a)]f(b)=f(b)g(a)−f(a)g(b)h(b)=[f(b)-f(a)]g(b)-[g(b)-g(a)]f(b)=f(b)g(a)-f(a)g(b).
Damit sind für die Funktion hh die Voraussetzungen des Satzes von Rolle erfüllt und es gibt ein x0∈]a,b[x_0\in ]a,b[ mit h′(x0)=0h'(x_0)=0. Nun ist
h′(x)=[f(b)−f(a)]g′(x)−[g(b)−g(a)]f ′(x)h'(x)=[f(b)-f(a)]g'(x)-[g(b)-g(a)]f\, '(x)
und
0=h′(x0)=[f(b)−f(a)]g′(x0)−[g(b)−g(a)]f ′(x0)0=h'(x_0)=[f(b)-f(a)]g'(x_0)-[g(b)-g(a)]f\, '(x_0),
und nach einer einfachen Umformung ergibt sich die Behauptung. □\qed
 
 

An Archimedes wird man sich erinnern, wenn Aischylos vergessen ist - weil zwar die Sprachen sterben, nicht aber die mathematischen Ideen.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Differentialrechnung