Satz von Rolle

Satz 15JD (Satz von Rolle)

Sei ff eine im abgeschlossenen Intervall [a,b][a,b] stetige Funktion und im offenen Intervall ]a,b[]a,b[ differenzierbar mit f(a)=f(b)f(a)=f(b), dann gibt es ein x0∈]a,b[x_0\in ]a,b[ mit f ′(x0)=0f\, '(x_0)=0.

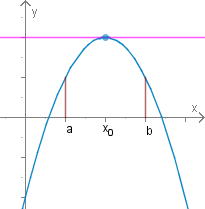
Rolle.png
Geometrische Deutung
Unter den Voraussetzungen des Satzes existiert eine zur x-Achse parallele Tangente an die Kurve.

Beweis

Da ff auf [a,b][a,b] stetig ist, nimmt die Funktion nach Satz 15FV ihr Minimum mm und Maximum MM an.
Fall 1: m=Mm=M: Dann ist ff konstant auf [a,b][a,b] und f ′(x)=0f\, '(x)=0 für alle x∈]a,b[x\in ]a,b[ (Satz 5317C). Wir wählen uns einen beliebigen Punkt x0∈]a,b[x_0\in ]a,b[ für den dann die Behauptung erfüllt ist.
Fall 2: m<Mm<M: Beide Werte werden angenommen. Wegen f(a)=f(b)f(a)=f(b) können aber nicht beide Werte in aa und bb angenommen werden. Es gibt also einen Punkt x0∈]a,b[x_0\in ]a,b[ für den f(x0)=mf(x_0)=m (oder f(x0)=Mf(x_0)=M) gilt. Nach Satz 15VE gilt für diesen Punkt f ′(x0)=0f\, '(x_0)=0. □\qed
 
 

Man darf nicht das, was uns unwahrscheinlich und unnatürlich erscheint, mit dem verwechseln, was absolut unmöglich ist.

Carl Friedrich Gauß

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Differentialrechnung