Arkussekans und Arkuskosekans

Arkussekans und Arkuskosekans sind mathem. Funktionen. Sie sind die Umkehrfunktionen der Sekansfunktion bzw. der Kosekansfunktion und damit Arkusfunktionen. Da die Sekans- und die Kosekansfunktion periodisch sind, wird zur Umkehrung der Definitionsbereich von Sekans auf [0 , π]\lbrack 0 \, , \, \pi \rbrack , und der Definitionsbereich von Kosekans auf [−π/2, π/2]\lbrack - {\pi / 2 }, \, \pi / 2 \rbrack beschränkt
Schreibweise:
f(x)=arcsec(x)f(x) = \mathrm{arcsec}(x)
f(x)=arccsc(x)f(x) = \mathrm{arccsc}(x)
 
 

Definition

Umkehrfunktionen zu Sekans und Kosekans

Eigenschaften

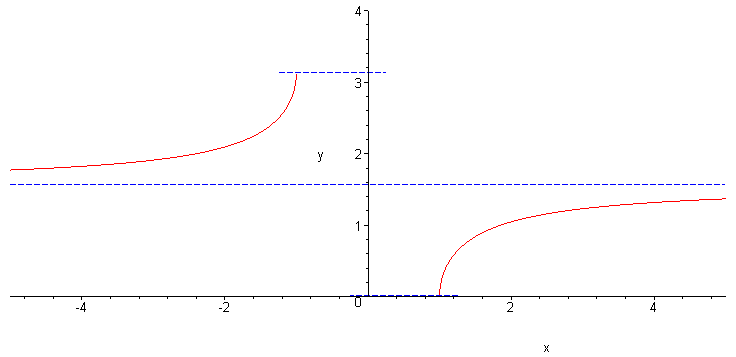
Arcsec.png
left
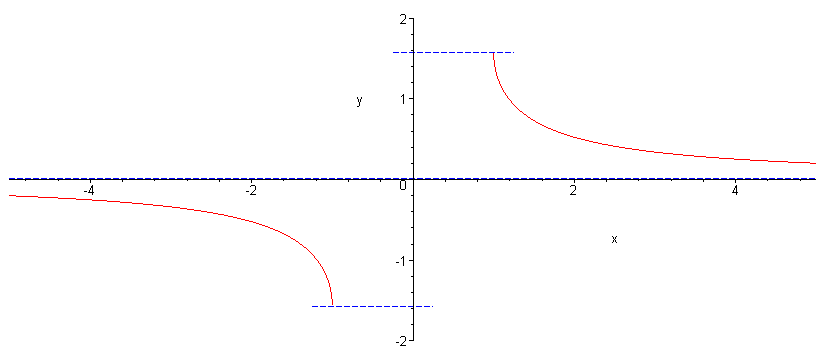
Arccsc.png
Arkussekans Arkuskosekans
Definitionsbereich −∞<x≤−1 , -\infty < x \le -1 \, , 1≤x<+∞ \, 1 \le x < +\infty −∞<x≤−1 , -\infty < x \le -1 \, , 1≤x<+∞ \, 1 \le x < +\infty
Wertebereich 0≤<f(x)≤π 0 \le < f(x) \le \pi −π2≤f(x)≤π2 - \dfrac{\pi}{2} \le f(x) \le \dfrac{\pi}{2}
Periodizität keine keine
Monotonie In beiden Abschnitten jeweils
streng monoton steigend 		In beiden Abschnitten jeweils
streng monoton fallend
Symmetrien Punktsymmetrie zum Punkt x=0,y=π2x = 0 , y = \dfrac{\pi}{2} Ungerade Funktion arccsc(x) \mathrm{arccsc}(x) =−arccsc(−x) = - \mathrm{arccsc}(-x)
Asymptoten f(x)→∓π2f(x) \to\mp \dfrac{\pi}{2} für x→±∞x \to\pm\infty f(x)→±π2f(x) \to\pm \dfrac{\pi}{2} für x→±∞x \to\pm\infty
Nullstellen keine keine
Sprungstellen keine keine
Polstellen keine keine
Extrema keine keine
Wendepunkte keine keine

Reihenentwicklung

Arkussekans:
arcsec(x)\mathrm{arcsec}(x)=π2−∑k=0∞(2k−1)!!x−(2k+1)(2k)!!∗(2k+1) =\dfrac{\pi}{2} - \sum\limits_{k=0}^{\infty} \dfrac{(2k-1)!! x^{-(2k+1)}} {(2k)!! * (2k+1) }≈π2−x−1−16x−3−340x−5 \approx\dfrac{\pi}{2}- x^{-1}-\dfrac{1}{6}x^{-3}-\dfrac{3}{40}x^{-5}
Arkuskosekans:
arccsc(x)=∑k=0∞(2k−1)!!x−(2k+1)(2k)!!⋅(2k+1)\mathrm{arccsc}(x)=\sum\limits_{k=0}^{\infty} \dfrac{(2k-1)!! x^{-(2k+1)}} {(2k)!! \cdot (2k+1) }

Umkehrfunktion

Arkussekans:
x=sec⁡(y)x = \sec(y)
Arkuskosekans:
x=csc⁡(y)x = \csc(y)

Ableitung

Arkussekans:
ddxarcsec(ax+b)\dfrac{d}{dx} \mathrm{arcsec}(ax+b) =a∣ax+b∣(ax+b)2−1 = \dfrac{a}{|ax+b| \sqrt{(ax+b)^2 - 1}}
Arkuskosekans:
ddxarccsc(ax+b)\dfrac{d}{dx} \mathrm{arccsc}(ax+b) =−ddxarcsec(ax+b) = -\dfrac{d}{dx} \mathrm{arcsec}(ax+b) =−a∣ax+b∣(ax+b)2−1 = - \dfrac{a}{|ax+b| \sqrt{(ax+b)^2 - 1}}

Integral

Arkussekans:
∫arcsec⁡(x)dx⁡\int\limits\operatorname{arcsec}(x)\operatorname{dx}=x⋅arcsec⁡(x)−ln⁡(x+x2−1) =x \cdot \operatorname{arcsec}(x) -\ln\braceNT{x+\sqrt{x^2-1}}
Arkuskosekans:
∫arccsc⁡(x)dx⁡\int\limits\operatorname{arccsc}(x)\operatorname{dx}=xarccsc⁡(x)+ln⁡(x+x2−1) =x\operatorname{arccsc}(x) +\ln\braceNT{x+\sqrt{x^2-1}}

Umrechnung

arcsecx=arccos⁡1x \mathrm{arcsec }x = \arccos \dfrac{1}{x}
arccscx=arcsin⁡1x \mathrm{arccsc }x = \arcsin \dfrac{1}{x}

Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Arkussekans und Arkuskosekans aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Transzendente Funktionen