Arkustangens und Arkuskotangens

Arkustangens und Arkuskotangens sind mathematische Funktionen. Sie sind die Umkehrfunktionen des Tangens bzw. des Kotangens und damit Arkusfunktionen. Da der Tangens periodisch ist, wird zur Umkehrung der Definitionsbereich von Tangens auf dem Intervall ]−π/2 , π/2[] - \pi / 2 \, , \, \pi / 2 [ beschränkt. Beim Arkuskotangens erfolgt eine Beschränkung auf 0≤f(x)≤π 0 \le f(x) \le \pi
 
 

Definition

Umkehrfunktion zu Tangens und Kotangens.
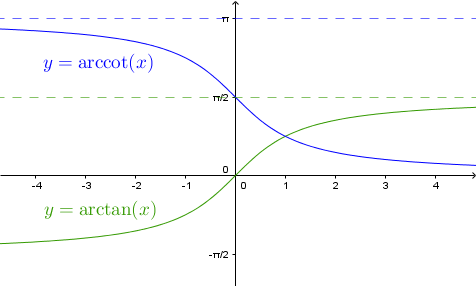
AtanAcot.png

Eigenschaften

Zwischen Arkustangens und Arkuskotangens besteht folgende Beziehung:
arccot⁡z=π2−arctan⁡z \arccot z = \dfrac{\pi}{2} - \arctan z .
Arkustangens Arkuskotangens
Definitionsbereich −∞<x<+∞ -\infty < x < +\infty −∞<x<∞ -\infty < x < \infty
Wertebereich −π2<f(x)<+π2-\dfrac{\pi}{2} < f(x) < + \dfrac{\pi}{2} 0≤f(x)≤π 0 \le f(x) \le \pi
Periodizität keine keine
Monotonie streng monoton steigend streng monoton fallend
Symmetrien Ungerade Funktion: arctan⁡(−x)=−arctan⁡x\arctan(-x) = -\arctan x Punktsymmetrie zu (x=0 , y=π2)(x=0 \, , \, y =\dfrac{\pi}{2})
arccot⁡x=π−arccot⁡(−x)\arccot x = \pi - \arccot(-x)
Asymptoten f(x)→±π2f(x) \to\pm \dfrac{\pi}{2} für x→±∞x \to\pm\infty f(x)→πf(x) \to \pi für x→−∞x \to -\infty
f(x)→0f(x) \to 0 für x→+∞x \to + \infty
Nullstellen x=0x = 0 keine
Sprungstellen keine keine
Polstellen keine keine
Extrema keine keine
Wendepunkte x=0x = 0 x=0x = 0

Spezielle Werte

xx −∞-\infty −3-\sqrt{3} −1-1 −13-\dfrac{1}{\sqrt{3}} 00 13\dfrac{1}{\sqrt{3}} 11 3\sqrt{3} ∞\infty
arctan⁡(x)\arctan(x) −π2-\dfrac{\pi}{2} −π3-\dfrac{\pi}{3} −π4-\dfrac{\pi}{4} −π6-\dfrac{\pi}{6} 00 π6\dfrac{\pi}{6} π4\dfrac{\pi}{4} π3\dfrac{\pi}{3} π2\dfrac{\pi}{2}

Reihenentwicklung

Die Taylorreihe des Arkustangens lautet:
arctan⁡x=∑k=0∞(−1)kx2k+12k+1 \arctan x=\sum\limits_{k=0}^{\infty} (-1)^k\dfrac{x^{2k+1}}{2k+1}=x−13x3+15x5−17x7+⋯ = x - \dfrac13 x^3 + \dfrac15 x^5 - \dfrac17 x^7+ \cdots
Diese Reihe konvergiert genau dann, wenn ∣x∣≤1|x|\le 1. Der Arkustangens ist allerdings auf ganz R\R definiert.
Die Reihenentwicklung kann zur näherungsweisen Berechnung der Zahl π\pi verwendet werden: Die einfachste Formel ist der Spezialfall x=1x=1, die Leibniz-Formel
π4=1−13+15−17+−…\dfrac\pi4=1-\dfrac13+\dfrac15-\dfrac17+-\ldots
Die kompliziertere Formel
π4=4arctan⁡15−arctan⁡1239\dfrac\pi4=4\arctan\dfrac15-\arctan\dfrac1{239}
verwendete John Machin[1] , um die ersten 100 Nachkommastellen von π\pi zu berechnen.
Die Taylorreihe des Arkuskotangens lautet:
arccot⁡x=π2−∑k=0∞(−1)k2k+1x2k+1 \arccot x=\dfrac{\pi}{2} - \sum\limits_{k=0}^{\infty} { \dfrac{(-1)^k}{2k+1} x^{2k+1}} \, = π2−x+13x3 = \, \dfrac{\pi}{2}- x + \dfrac{1}{3}x^3 −15x5+17x7⋯ - \dfrac15 x^5 + \dfrac17 x^7 \cdots

Funktionalgleichung

Die Arkustangenswerte über 11 lassen sich aus den Werten zwischen 0 und 1 ableiten:
arctan⁡1x=π2−arctan⁡x\arctan \dfrac{1}{x} = \dfrac{\pi}{2} - \arctan x
Das geht auch mit Werten für x<0x < 0:
arctan⁡1x=−π2−arctan⁡x\arctan \dfrac{1}{x} = -\dfrac{\pi}{2} - \arctan x

Umkehrfunktionen

Tangensfunktion und Kotangensfunktion:
x=tan⁡yx = \tan y und x=cot⁡y  x = \cot y \,

Ableitungen

Arkustangens:
ddxarctan⁡(x)=11+x2\dfrac{\mathrm d}{\mathrm dx}\arctan(x)=\dfrac{1}{1+x^2}
ddxarctan⁡(ax+b)=a1+(ax+b)2\dfrac{\mathrm d}{\mathrm dx} \arctan(ax+b) = \dfrac{a}{1+(ax+b)^2}
Arkuskotangens:
arccot⁡′(x)=−11+x2{\arccot}' (x)=-\dfrac{1}{1+x^2}.
ddxarccot⁡(ax+b)=−ddxarctan⁡(ax+b)=−a1+(ax+b)2\dfrac{\mathrm d}{\mathrm dx} \arccot(ax+b) = - \dfrac{\mathrm d}{\mathrm dx} \arctan(ax+b)= - \dfrac{a}{1 + (ax+b)^2}

Stammfunktionen

Arkustangens:
Der Arkustangens spielt eine wesentliche Rolle bei der symbolischen Integration von Ausdrücken der Form
1ax2+bx+c \dfrac1{ax^2+bx+c}\, .
Ist die Diskriminante D=b2−4acD=b^2-4ac positiv oder Null, so kann man eine Stammfunktion mittels Partialbruchzerlegung bestimmen. Ist die Diskriminante negativ, so kann man den Ausdruck durch die Substitution
u=2ax+b−Du=\dfrac{2ax+b}{\sqrt{-D}}
in die Form
4a−D 11+u2\dfrac{4a}{-D} \, \dfrac1{1+u^2}
bringen; eine Stammfunktion ist also
2−Darctan⁡2ax+b−D \dfrac2{\sqrt{-D}}\arctan\dfrac{2ax+b}{\sqrt{-D}}\, .
Eine Stammfunktion des Arkustangens selbst ist
∫arctan⁡xa dx,=x arctan⁡xa−a2ln⁡(a2+x2) \int\limits \arctan \dfrac{x}{a} \, \mathrm dx, = x \, \arctan \dfrac{x}{a} - \dfrac{a}{2} \ln\braceNT{a^2 + x^2}\,
Arkuskotangens:
F(x)=x arccot⁡x+12 ln⁡(1+x2)+CF(x) = x \, \arccot x + \dfrac{1}{2} \, \ln \braceNT{ 1 + x^2 } + C
∫arccot⁡xa dx=x arccot⁡xa+a2 ln⁡(a2+x2) \int\limits \arccot \dfrac{x}{a} \, dx= x \, \arccot \dfrac{x}{a} + \dfrac{a}{2} \, \ln(a^2 + x^2)

Näherungsweise Berechnung

Es gelten folgende Näherungen:
arctan⁡x≈3x3+x2 \arctan x \approx \dfrac{3x}{3+x^2} für ∣x∣<1|x|<1,
arccot⁡x≈3x3x2−1 \arccot x \approx \dfrac{3x}{3x^2-1} für x≫1x\gg 1.
 
1  John Machin, 1680-1751, englischer Astronom und Mathematiker

Wer die erhabene Weisheit der Mathematik tadelt, nährt sich von Verwirrung.

Leonardo da Vinci

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Arkustangens und Arkuskotangens aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Transzendente Funktionen