Dualräume

Sei VV ein Vektorraum über dem Körper KK. Fasst man KK als Vektorraum über sich selbst auf, so heißen die Vektorraumhomomorphismen f:V→Kf:V\rightarrow K Linearformen.
Nach Satz 15XW bilden diese Homomorphismen einen Vektorraum Hom(V,K)\Hom(V,K). Dieser Vektorraum heißt der Dualraum (oder duale Vektorraum) zu VV und wird mit V∗V^* bezeichnet. Der Dualraum ist also ein spezieller Vektorraum von Homomorphismen, nämlich derjenige, der aus den Linearformen von VV besteht.

Satz 15YJ (Dimension des Dualraums)

Sei VV ein endlich dimensionaler Vektorraum über dem Körper KK. Die Dimension des Dualraums V∗V^* stimmt mit der von VV überein, also:
dim⁡V∗=dim⁡V\dim V^*=\dim V

Beweis

Mit Folgerung 15YH gilt: dim⁡V∗=dim⁡Hom(V,K)\dim V^*=\dim \Hom(V,K) =dim⁡V⋅dim⁡K=\dim V\cdot\dim K =dim⁡V⋅1=dim⁡V=\dim V\cdot 1=\dim V □\qed

Duale Abbildung

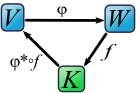
DAbb.png
Jede Abbildung φ:V→W\varphi:V\rightarrow W liefert eine duale Abbildung φ∗:W∗→V∗ \varphi^*:W^*\rightarrow V^* mit (f:W→K)↦(φ∗(f):V→K) (f:W\rightarrow K)\mapsto (\varphi^*(f):V\rightarrow K), die folgendermaßen definiert ist
(φ∗(f))(v):=f(φ(v)) (\varphi^*(f))(v):=f(\varphi(v)).
Es gilt φ∗(f)=f∘φ \varphi^*(f)=f\circ \varphi.
 
 

Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Lineare Algebra