Satz von Ptolemäus

Der Satz von Ptolemäus stellt für Sehnenvierecke eine Beziehung zwischen den Längen der Diagonalen und den Seitenlängen her.

Satz 5517A (Satz von Ptolemäus)

In einem Sehnenviereck ist das Produkt der Diagonalenlängen gleich der Summe der Produkte der Längen der gegenüberliegenden Seiten:
ef=ac+bdef=ac+bd.

Beweis

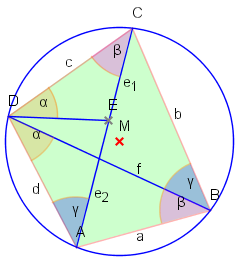
Ptole.png
Wir tragen den Winkel α=∠ADB\alpha=\angle ADB an der Seite cc an. Dies ist obdA. für eine Ecke (in unserem Fall D) möglich. Der Schenkel des neu entstandenen Winkels scheide die Diagonale AC‾\overline{AC} im Punkt EE. Die Diagonalenabschnitte werden mit e1e_1 und e2e_2 bezeichnet.
Nach dem Peripheriewinkelsatz sind die in der Grafik mit β\beta und γ\gamma bezeichneten Winkel jeweils gleich groß. Daher sind auch die Dreiecke △DEC\triangle DEC und △DAB\triangle DAB ähnlich. Es gilt also
fa=ce1\dfrac f a=\dfrac c {e_1}.(1)
Auch die Dreiecke △DAE\triangle DAE und △DBC\triangle DBC sind ähnlich. Sie stimmen neben γ\gamma auch im Winkel α\alpha ergänzt um den Winkel ∠EDB\angle EDB überein. Wir erhalten dann die folgende Proportionalität:
fb=de2\dfrac f b=\dfrac d {e_2}.(2)
Die Gleichung (1) und (2) stellen wir zu
fe1=acfe_1=ac(3)
und
fe2=bdfe_2=bd(4)
um.
Addieren wir diese, erhalten wir die Behauptung:
ef=(e1+e2)f=ac+bdef=(e_1+e_2)f=ac+bd
□\qed
 
 

Es ist unglaublich, wie unwissend die studirende Jugend auf Universitäten kommt, wenn ich nur 10 Minuten rechne oder geometrisire, so schläft 1/4 derselben sanft ein.

Georg Christoph Lichtenberg

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Viereck