Sehnensatz

Satz 5516E (Sehnensatz/ Diagonalenabschnitte im Sehnenviereck)

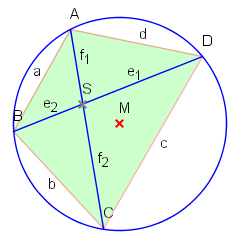
SehnenviereckDiag.png
Im Sehnenviereck gilt für die Diagonalenabschnitte
e1⋅e2=f1⋅f2e_1\cdot e_2=f_1\cdot f_2
Dieser Satz wird als Sehnensatz am Kreis wie folgt formuliert: Die Produkte der Sehnenabschnitte sind gleich groß.
Er ergibt sich sofort, wenn man die Diagonalen AC‾\overline {AC} und BD‾\overline {BD} als Sehnen auffasst.

Beweis

Wir zeigen zuerst, dass die Dreiecke △ASD\triangle ASD und △CSB\triangle CSB ähnlich sind. Es gilt
∠ASD=∠CSB\angle ASD=\angle CSB,
da sie Scheitelwinkel sind. Außerdem ergibt sich aus dem Peripheriewinkelsatz, dass
∠SBC=∠DAS\angle SBC=\angle DAS.
Damit stimmen die Dreiecke in zwei Winkeln überein und sind ähnlich. Es gilt also
e1f2=f1e2\dfrac {e_1}{f_2}=\dfrac{f_1}{e_2},
woraus die Behauptung sofort ersichtlich ist.□\qed
 
 

Eine mathematische Wahrheit ist an sich weder einfach noch kompliziert, sie ist.

Émile Lemoine

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Viereck