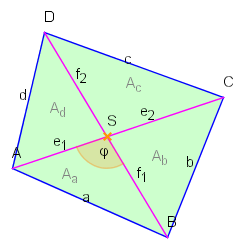
Flächeninhalt des Sehnenvierecks
Den Flächeninhalt des
Sehnenvierecks kann man durch eine einfache, nur von den Seiten abhängende, Formel ermitteln.
Formel 5518F (Brahmagupta)
A = ( s − a ) ( s − b ) ( s − c ) ( s − d ) A=\sqrt{(s-a)(s-b)(s-c)(s-d)} A = ( s − a ) ( s − b ) ( s − c ) ( s − d ) ,
wobei
s s s der halbe Umfang ist:
s = a + b + c + d 2 s=\dfrac {a+b+c+d} 2 s = 2 a + b + c + d .
Herleitung
A = 1 2 ⋅ e f ⋅ sin φ A=\dfrac 1 2\cdot ef\cdot \sin\phi A = 2 1 ⋅ e f ⋅ sin φ .
(1) Quadrieren wir diese Gleichung und multiplizieren sie mit 16, ergibt sich
16 ⋅ A 2 = 4 ⋅ e 2 f 2 ⋅ sin 2 φ 16\cdot A^2=4\cdot e^2f^2\cdot \sin^2\phi 1 6 ⋅ A 2 = 4 ⋅ e 2 f 2 ⋅ sin 2 φ ,
(2) 16 ⋅ A 2 = 4 ⋅ e 2 f 2 ( 1 − cos 2 φ ) 16\cdot A^2=4\cdot e^2f^2(1-\cos^2\phi) 1 6 ⋅ A 2 = 4 ⋅ e 2 f 2 ( 1 − cos 2 φ ) = 4 ( a c + b d ) 2 − 4 ⋅ e 2 f 2 cos 2 φ =4(ac+bd)^2-4\cdot e^2f^2\cos^2\phi = 4 ( a c + b d ) 2 − 4 ⋅ e 2 f 2 cos 2 φ .
(3) Jetzt wenden wir den
Kosinussatz auf die einzelnen Teildreiecke an und erhalten:
a 2 = e 1 2 + f 1 2 − 2 e 1 f 1 cos φ a^2={e_1}^2+{f_1}^2-2 e_1 f_1\cos\phi a 2 = e 1 2 + f 1 2 − 2 e 1 f 1 cos φ (4) b 2 = f 1 2 + e 2 2 + 2 f 1 e 2 cos φ b^2={f_1}^2+{e_2}^2+2 f_1 e_2\cos\phi b 2 = f 1 2 + e 2 2 + 2 f 1 e 2 cos φ (5) c 2 = e 2 2 + f 2 2 − 2 e 2 f 2 cos φ c^2={e_2}^2+{f_2}^2-2 e_2 f_2\cos\phi c 2 = e 2 2 + f 2 2 − 2 e 2 f 2 cos φ (6) d 2 = f 2 2 + e 1 2 + 2 f 2 e 1 cos φ d^2={f_2}^2+{e_1}^2+2 f_2 e_1\cos\phi d 2 = f 2 2 + e 1 2 + 2 f 2 e 1 cos φ .
(7) Dabei steckt in
(5) und
(7) die Beziehung
cos ( 180 ° − φ ) = − cos φ \cos(180°-\phi)=\uminus\cos\phi cos ( 1 8 0 ° − φ ) = − cos φ .
− a 2 + b 2 − c 2 + d 2 = 2 e f cos φ -a^2+b^2-c^2+d^2=2 e f\cos\phi − a 2 + b 2 − c 2 + d 2 = 2 e f cos φ ,
(8) was wir in
(3) einsetzen, um
16 ⋅ A 2 = 4 ( a c + b d ) 2 − ( − a 2 + b 2 − c 2 + d 2 ) 2 16\cdot A^2=4(ac+bd)^2-(-a^2+b^2-c^2+d^2)^2 1 6 ⋅ A 2 = 4 ( a c + b d ) 2 − ( − a 2 + b 2 − c 2 + d 2 ) 2 = [ 2 ( a c + b d ) + ( − a 2 + b 2 − c 2 + d 2 ) ] [ 2 ( a c + b d ) − ( − a 2 + b 2 − c 2 + d 2 ) ] =\ntxbraceL{2(ac+bd)+(\uminus a^2+b^2-c^2+d^2)}\ntxbraceL{2(ac+bd)-(\uminus a^2+b^2-c^2+d^2)} = [ 2 ( a c + b d ) + ( − a 2 + b 2 − c 2 + d 2 ) ] [ 2 ( a c + b d ) − ( − a 2 + b 2 − c 2 + d 2 ) ] = [ − ( a − c ) 2 + ( b + d ) 2 ] [ ( a + c ) 2 − ( b − d ) 2 ] =\ntxbraceL{\uminus(a-c)^2+(b+d)^2}\ntxbraceL{(a+c)^2-(b-d)^2} = [ − ( a − c ) 2 + ( b + d ) 2 ] [ ( a + c ) 2 − ( b − d ) 2 ] = ( a − c + b + d ) ( − a + c + b + d ) ( a + c + b − d ) ( a + c − d + b ) =(a-c+b+d)(-a+c+b+d)(a+c+b-d)(a+c-d+b) = ( a − c + b + d ) ( − a + c + b + d ) ( a + c + b − d ) ( a + c − d + b ) = 2 ( s − c ) ⋅ 2 ( s − a ) ⋅ 2 ( s − d ) ⋅ 2 ( s − b ) =2(s-c)\cdot 2(s-a)\cdot 2(s-d)\cdot 2(s-b) = 2 ( s − c ) ⋅ 2 ( s − a ) ⋅ 2 ( s − d ) ⋅ 2 ( s − b ) = 16 ( s − c ) ( s − a ) ( s − d ) ( s − b ) =16(s-c)(s-a)(s-d)(s-b) = 1 6 ( s − c ) ( s − a ) ( s − d ) ( s − b ) (9)
zu erhalten, woraus sich sofort die Behauptung ergibt.
□ \qed □
Ich glaube, daß es, im strengsten Verstand, für den Menschen nur eine einzige Wissenschaft gibt, und diese ist reine Mathematik. Hierzu bedürfen wir nichts weiter als unseren Geist.
Georg Christoph Lichtenberg
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе