Normalverteilung
Die Normal- oder Gaußverteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß-Funktion, Gauß-Kurve, Gauß-Glocke oder Glockenkurve genannt.
Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, der besagt, dass eine Summe von unabhängigen, identisch verteilten Zufallsvariablen im Grenzwert normalverteilt ist. Das bedeutet, dass man Zufallsvariablen dann als normalverteilt ansehen kann, wenn sie durch Überlagerung einer großen Zahl von Einflüssen entstehen, wobei jede einzelne Einflussgröße einen im Verhältnis zur Gesamtsumme unbedeutenden Beitrag liefert.
Viele natur-, wirtschafts- und ingenieurswissenschaftliche Vorgänge lassen sich durch die Normalverteilung entweder exakt oder wenigstens in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).
Zufallsgrößen mit Normalverteilung benutzt man zur Beschreibung zufälliger Versuche bei der Bestimmung von Geschwindigkeiten, Messfehlern, Beobachtungsfehlern wie:
- zufällige Beobachtungs- und Messfehler.
- zufällige Abweichungen vom Nennmaß bei der Fertigung von Werkstücken.
- Beschreibung der Brownschen Molekularbewegung.
In der Versicherungsmathematik ist die Normalverteilung geeignet zur Modellierung von Schadensdaten im Bereich mittlerer Schadenshöhen.
Definition
heißt --normalverteilt, auch geschrieben als oder -normalverteilt, wobei der Erwartungswert und die Standardabweichung sind.
Die Verteilungsfunktion der Normalverteilung ist gegeben durch
- .
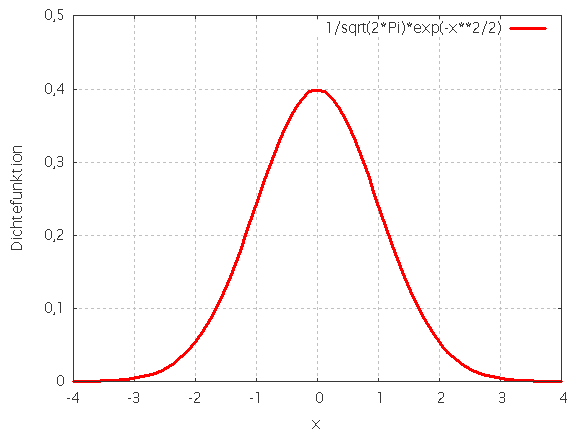
So sieht die Dichtefunktion einer Standardnormalverteilung aus. Angegeben sind die Intervalle im Abstand 1, 2 und 3 Standardabweichungen vom Erwartungswert 0, die rund 68%, 95,5% und 99,7% der Fläche unter der Glockenkurve umfassen. Die gleichen Prozentsätze gelten für alle Normalverteilungen in Bezug auf die entsprechenden Erwartungswerte und Standardabweichungen.
Die Normalverteilung ist eine Grenzverteilung, die nicht direkt beobachtet werden kann. Die Annäherung verläuft aber mit wachsendem n sehr schnell, so dass schon die Verteilung einer Summe von 30 oder 40 unabhängigen, identisch verteilten Zufallsgrößen einer Normalverteilung recht ähnlich ist.
Die Glockenkurve schmückte, neben dem Portrait von Carl Friedrich Gauß platziert, von 1989 bis 2001 die 10-DM-Banknote der Bundesrepublik Deutschland.
Eigenschaften
Symmetrie
Der Graph der Wahrscheinlichkeitsdichte ist eine Gauß'sche Glockenkurve, welche symmetrisch zum Wert von ist und deren Höhe und Breite von abhängt. Mathematisch ausgedrückt wird diese Symmetrie durch
und
- .
Maximalwert und Wendepunkte der Dichtefunktion
Mit Hilfe der ersten und zweiten Ableitung lassen sich der Maximalwert und die Wendepunkte bestimmen.
Somit liegen die Wendepunkte der Dichtefunktion bei .
Normierung
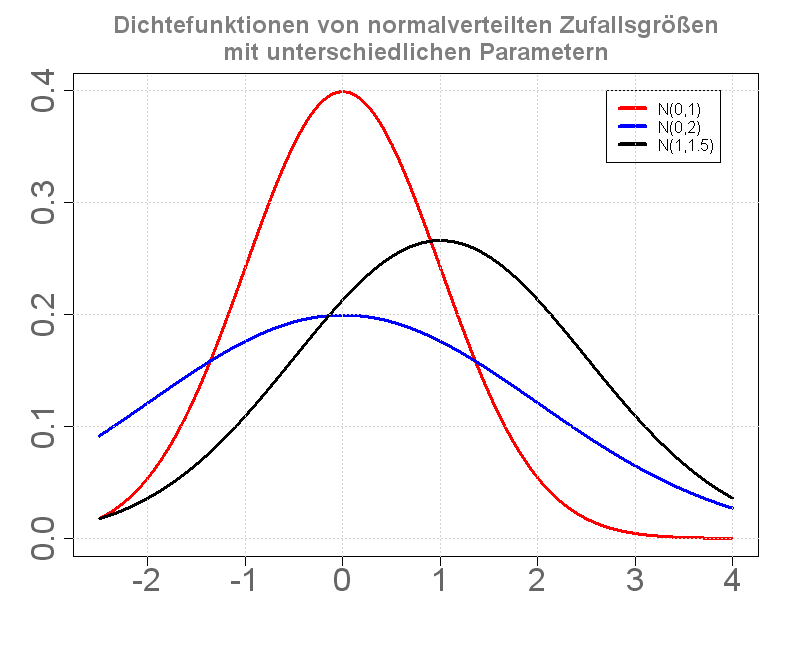
Wichtig ist, dass die gesamte Fläche unter der Kurve gleich 1 ist, also der Wahrscheinlichkeit eines sicheren Ereignisses entspricht. Somit folgt, dass wenn zwei Gauß'sche Glockenkurven dasselbe , aber unterschiedliche -Werte haben, jene Kurve mit dem größeren breiter und niedriger ist (da ja beide zugehörigen Flächen jeweils den Wert von 1 haben und nur die Standardabweichung (oder " Streuung") höher ist). Zwei Glockenkurven mit dem gleichen , aber unterschiedlichen haben gleich aussehende Graphen, die jedoch auf der x-Achse um die Differenz der -Werte zueinander verschoben sind.
Da sich das Integral der Wahrscheinlichkeitsdichtefunktion nicht auf eine elementare Stammfunktion zurückführen lässt, wurde für die Berechnung früher meist auf Tabellen zurückgegriffen; heutzutage sind entsprechende Zellenfunktionen in üblichen Tabellenkalkulationsprogrammen stets verfügbar. Tabellen wie Zellenfunktionen gelten aber in der Regel nicht für beliebige - und -Werte, sondern nur für die Standardnormalverteilung, bei der und ist (man spricht auch von einer 0-1-Normalverteilung oder normierten Normalverteilung).
Die Tabellen sind also für die Wahrscheinlichkeitsfunktion (auch Gauß'sches Fehlerintegral genannt) mit
ausgelegt. Analog dazu wird die zugehörige normierte Wahrscheinlichkeitsdichtefunktion mit bezeichnet.
Ist nun eine beliebige --Verteilung gegeben, so muss diese nur in eine Standardnormalverteilung transformiert werden.
Erwartungswert
Die Normalverteilung besitzt den Erwartungswert
- .
Varianz und Standardabweichung
Die Varianz ergibt sich analog zu
- .
Für die Standardabweichung ergibt sich
- .
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten
- .
Schiefe
Charakteristische Funktion
Die charakteristische Funktion für hat die Form
- .
Für die Standardnormalverteilung vereinfacht sich die charakteristische Funktion zu
- .
Momenterzeugende Funktion
Die momenterzeugende Funktion der Normalverteilung ist
- .
Invarianz gegenüber Faltung
Die Normalverteilung ist invariant gegenüber der Faltung, d. h. die Faltung einer Gaußkurve der Halbwertsbreite mit einer Gaußkurve der Halbwertsbreite ergibt wieder eine Gaußkurve mit der Halbwertsbreite .
Anders gesprochen, die Summe zweier unabhängiger normalverteilter Zufallsgrößen ist wieder normalverteilt. Speziell ist das arithmetische Mittel unabhängiger und identisch normalverteilter Zufallsgrößen mit den Parametern wieder eine normalverteilte Zufallsgröße mit und .
Die Dichtefunktion der Normalverteilung ist ein Fixpunkt der Fourier-Transformation, d.h. die Fourier-Transformierte einer Gaußkurve ist wieder eine Gaußkurve. Das Produkt der Standardabweichungen dieser korrespondierenden Gaußkurven ist konstant; es gilt die Heisenbergsche Unschärferelation.
Entropie
Mehrdimensionale Verallgemeinerung
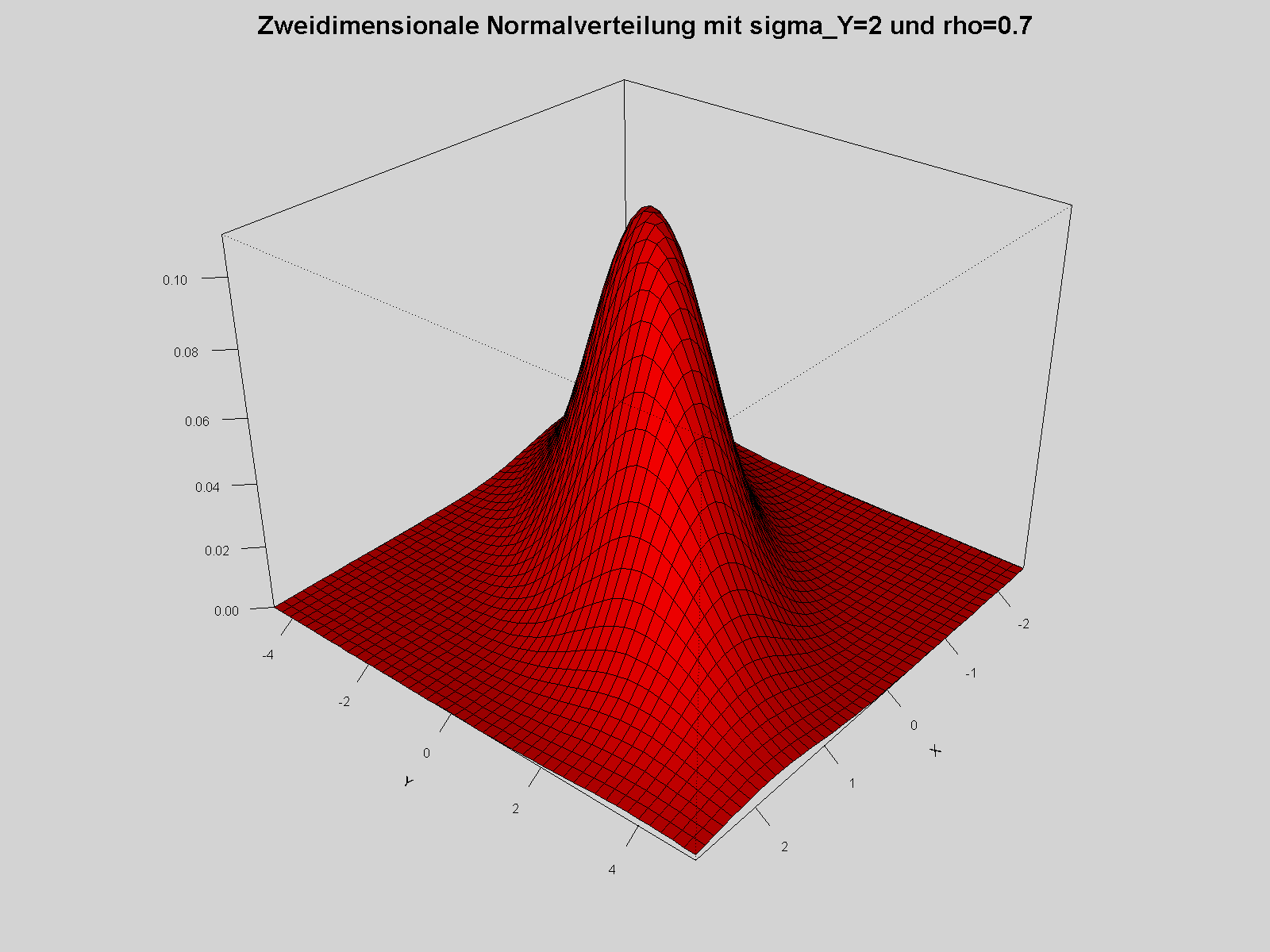
Dichte der zweidimensionalen Normalverteilung; die Standardabweichung der zweiten Koordinate Y ist 2, die Korrelation zwischen den Koordinaten 0.7
Das Wahrscheinlichkeitsmaß auf , das durch die Dichtefunktion
definiert wird, heißt Standardnormalverteilung der Dimension . Ein Zufallsvektor ist genau dann standardnormalverteilt auf , wenn seine Komponenten standardnormalverteilt und stochastisch unabhängig sind.
Ein Wahrscheinlichkeitsmaß auf heißt -dimensionale Normalverteilung, wenn eine Matrix und ein Vektor existieren, so dass mit der affinen Abbildung gilt: .
Die multivariate Normalverteilung ist die einzige rotationssymmetrische multivariate Verteilung, deren Komponenten stochastisch unabhängig sind.
Die Dichtefunktion der zweidimensionalen Normalverteilung mit einem Korrelationskoeffizienten ist
und schließlich im -dimensionalen Fall
Beziehungen zu anderen Verteilungsfunktionen
Transformation zur Standardnormalverteilung (z-Transformation)
Ist eine Normalverteilung mit beliebigen und gegeben, so kann diese durch eine Transformation auf eine -Normalverteilung zurückgeführt werden. Dazu wird die Verteilungsfunktion der allgemeinen Normalverteilung mit substituiert und die Integralgrenzen werden angepasst:
| Nebenrechnung für die Substitution |
Wird nun definiert und durch ersetzt, so erhält man die Verteilungsfunktion der Standardnormalverteilung:
Geometrisch betrachtet entspricht die durchgeführte Substition einer flächentreuen Transformation der Glockenkurve von zur Glockenkurve von .
Approximation der Binomialverteilung durch die Normalverteilung
Die Normalverteilung kann zur Approximation der Binomialverteilung verwendet werden, wenn der Stichprobenumfang hinreichend groß und in der Grundgesamtheit der Anteil der gesuchten Eigenschaft nicht zu klein ist. Als Faustregel dafür gilt: .
Allgemeines
Um 1900 postulierte Max Planck das Energiequantum , um die Energieverteilung der schwarzen Strahlung erklären zu können und es wurde daraufhin in vielen anderen Erscheinungen der Natur wiederentdeckt. Der bis dahin geltende Satz 'natura non facit saltus' - die Natur macht keine Sprünge - wurde wirksam widerlegt und zeigt auch, dass viele Phänomene, die oberflächlich für stetig gehalten werden, bei sehr genauer Betrachtung doch nichtstetig bzw. sprunghaft sind. Die Normalverteilung liefert für diese Vorgänge eine sehr gute Approximation, denn viele endliche Zufallsvariablen sind näherungsweise normalverteilt. Eine in der Natur oft anzutreffende Wahrscheinlichkeitsverteilung ist die Binomialverteilung. Auch sie lässt sich in sehr guter Näherung mit der Normalverteilung beschreiben. Mathematisch wird dies durch den Grenzwertsatz belegt. Er besagt in diesem Fall, dass sich die nichtstetige Wahrscheinlichkeitsverteilung, die sich aus voneinander unabhängigen Zufallsgrößen ergibt, mit steigenden immer besser an die Normalverteilung angleicht. ist dabei die Anzahl der voneinander unabhängigen Zufallsversuche, von denen jeder einzelne eine Zufallsgröße ergibt.
Ein Beispiel für diese Angleichung der Häufigkeitsverteilung an die Normalverteilung ist folgender Würfelversuch: Gegeben seien zwei normale Würfel, wobei jeder eine Augenzahl von eins bis sechs aufweist. Sie sollen nun mal geworfen werden, d. h. es werden voneinander unabhängige Zufallsversuche durchgeführt. Bei jedem Versuch berechnet sich das Ergebnis aus der Gesamtanzahl der geworfenen Augen. Insgesamt werden einige hundert Würfe gemacht, wobei die Anzahl der gleichen Ergebnisse gezählt wird. Diese Häufigkeit kann anschließend in ein Diagramm eingetragen werden. Die resultierende Verteilung ist bei sehr wenigen Würfen rein zufällig, bei sehr hohen wird sie hingegen der Gauß'schen Glockenkurve (mit dem Erwartungswert von 7) immer ähnlicher, trotzdem ist sie immer noch diskret verteilt (d. h. der Graph besteht aus kleinen Stufen).
Approximation
Ist eine Binomialverteilung (siehe auch Bernoulli-Versuch) mit voneinander unabhängigen Stufen (bzw. Zufallsversuchen) mit einer Erfolgswahrscheinlichkeit gegeben, so lässt sich die Wahrscheinlichkeit für Erfolge allgemein durch für berechnen (wobei ist).
Für sehr große Werte von kann diese Binomialverteilung durch eine Normalverteilung approximiert werden (zentraler Grenzwertsatz). Dabei ist
- der Erwartungswert
- und die Standardabweichung
Ist nun , dann ist folgende Näherung brauchbar:
Bei der Normalverteilung wird die untere Grenze um 0,5 verkleinert und die obere Grenze um 0,5 vergrößert, um eine bessere Approximation bei einer geringen Standardabweichung gewährleisten zu können. Dies nennt man auch Stetigkeitskorrektur. Nur wenn einen sehr hohen Wert besitzt, kann auf sie verzichtet werden.
Da die Binomialverteilung diskret ist, muss auf einige Punkte geachtet werden:
- oder (und auch größer und größer gleich) müssen beachtet werden (was ja bei der Normalverteilung nicht der Fall ist). Deshalb muss bei die nächstkleinere natürliche Zahl gewählt werden, d. h.
- bzw.
- damit mit der Normalverteilung weitergerechnet werden kann.
- z. B.
- Außerdem ist
- (unbedingt mit Stetigkeitskorrektur)
- und lässt sich somit durch die oben angegebene Formel berechnen.
Der große Vorteil der Approximation liegt darin, dass sehr viele Stufen einer Binomialverteilung sehr schnell und einfach bestimmt werden können.
Beziehung zur Cauchy-Verteilung
Beziehung zur Chi-Quadrat-Verteilung
- Die Summe von unabhängigen quadrierten standardnormalverteilten Zufallsvariablen genügt einer Chi-Quadrat-Verteilung mit Freiheitsgraden.
- Die Summe mit von unabhängigen quadrierten standardnormalverteilten Zufallsvariablen genügt einer Chi-Quadrat-Verteilung mit Freiheitsgraden.
Die Chi-Quadrat-Verteilung wird zur Konfidenzschätzung für die Varianz einer normalverteilten Grundgesamtheit verwendet.
Beziehung zur logarithmischen Normalverteilung
Ist die Zufallsvariable normalverteilt mit , dann ist die Zufallsvariable logarithmisch-normalverteilt mit .
Die Entstehung einer logarithmischen Normalverteilung ist auf multiplikatives, die einer Normalverteilung auf additives Zusammenwirken vieler Zufallsgrößen zurückführen.
Beziehung zur F-Verteilung
mit besitzen, dann unterliegt die Zufallsvariable
einer F-Verteilung mit Freiheitsgraden. Dabei sind
- .
Beziehung zur Students-t-Verteilung
Wenn die unabhängigen Zufallsvariablen identisch normalverteilt sind mit den Parametern und , dann unterliegt die stetige Zufallsgröße
einer Students t-Verteilung mit Freiheitsgraden.
Die Students t-Verteilung wird zur Konfidenzschätzung für den Erwartungswert einer normalverteilten Zufallsvariable bei unbekannter Varianz verwendet.
Rechnen mit der Standardnormalverteilung
Bei Aufgabestellungen, bei denen die Wahrscheinlichkeit für normalverteilte Zufallsvariablen durch die Standardnormalverteilung ermittelt werden soll, ist es nicht nötig, die oben angegebene Transformation jedesmal durchzurechnen. Stattdessen wird einfach das Ergebnis der Transformation verwendet, um die Grenzen und die Zufallsvariable auf die Grenzen und die Zufallsvariable anzugleichen. Somit kann eine Verteilung durch
- beziehungsweise
zu transformiert werden.
Die Wahrscheinlichkeit für ein Ereignis, welches z. B. innerhalb der Werte und (für den Erwartungswert und die Standardabweichung ) liegt, ist durch folgende Umrechnung gleich der Wahrscheinlichkeit der Standardnormalverteilung mit den neuen Grenzen und :
( steht für die englische Bezeichnung "probability" oder das französische Wort "probabilité" der Wahrscheinlichkeit.)
Grundlegende Fragestellungen
Allgemein gibt die Verteilungsfunktion die Fläche unter der Glockenkurve bis zum Wert an, d. h. es wird das bestimmte Integral von bis berechnet.
Dies entspricht in Aufgabenstellungen einer gesuchten Wahrscheinlichkeit, bei der die Zufallsvariable kleiner oder kleiner gleich einer bestimmten Zahl ist. Durch die Verwendung der reellen Zahlen und der Stetigkeit der Normalverteilung macht es keinen Unterschied, ob nun oder verlangt ist,
- weil und somit .
Dasselbe gilt für größer und größer gleich.
Dadurch, dass nur kleiner oder größer einer Grenze (oder innerhalb oder außerhalb zweier Grenzen) liegen kann, ergeben sich für Aufgaben bei normalverteilten Wahrscheinlichkeitsberechnungen folgende zwei grundlegende Fragestellungen:
- Wie hoch ist die Wahrscheinlichkeit, dass bei einem Zufallsversuch die normalverteilte Zufallsvariable höchstens den Wert annimmt?
- In der Schulmathematik wird für diese Aussage auch die Bezeichnung Linker Spitz verwendet, da die Fläche unter der Gaußkurve von links bis zur Grenze verläuft. Für sind auch negative Werte erlaubt, trotzdem haben viele Tabellen der Standardnormalverteilung nur positive Einträge. Durch die Symmetrie der Kurve und der Negativitätsregel des linken Spitz stellt dies aber keine Einschränkung dar:
| (Anm.: Das Minus von wird im folgenden explizit |
| ausgedrückt, d.h. , wenn ) |
- Wie hoch ist die Wahrscheinlichkeit, dass bei einem Zufallsversuch die normalverteilte Zufallsvariable mindestens den Wert annimmt?
- Analog wird hier oft die Bezeichnung Rechter Spitz verwendet. Ebenso gibt es eine Negativitätsregel:
(Da jede Zufallsvariable der allgemeinen Normalverteilung sich in die Zufallsgröße der Standardnormalverteilung umwandeln lässt, gelten die Fragestellungen für beide Größen gleichbedeutend.)
Streubereich und Antistreubereich
Der Streubereich gibt die Wahrscheinlichkeit wieder, dass die normalverteilte Zufallsvariable Werte zwischen und annimmt:
Beim Sonderfall des symmetrischen Streubereiches ( , mit ) gilt:
Hingegen gibt der Antistreubereich die Höhe der Wahrscheinlichkeit an, dass die normalverteilte Zufallsvariable Werte außerhalb des Bereichs zwischen und annimmt:
- oder
Somit folgt bei einem symmetrischen Antistreubereich:
- oder
Streubereiche am Beispiel der Qualitätssicherung
Besondere Bedeutung haben beide Streubereiche z.B. bei der Qualitätssicherung von technischen oder wirtschaftlichen Produktionsprozessen. Hier gibt es einzuhaltende Toleranzgrenzen und , wobei es meist einen größten noch akzeptablen Abstand vom Erwartungswert (= dem optimalen Sollwert) gibt. kann hingegen empirisch aus dem Produktionsprozess gewonnen werden.
Wurde als einzuhaltendes Toleranzintervall angegeben, so liegt (je nach Fragestellung) ein symmetrischer Streu- oder Antistreubereich vor.
Im Falle des Streubereiches gilt:
Der Antistreubereich ergibt sich dann aus
oder wenn kein Streubereich berechnet wurde durch
- .
Das Ergebnis ist also die Wahrscheinlichkeit für verkaufbare Produkte, während die Wahrscheinlichkeit für Ausschuss bedeutet, wobei beides von den Vorgaben von und abhängig ist.
Ist bekannt, dass die maximale Abweichung symmetrisch um den Erwartungswert liegt, so sind auch Fragestellungen möglich, bei denen die Wahrscheinlichkeit vorgegeben und eine der anderen Größen zu berechnen ist.
Testen auf Normalverteilung
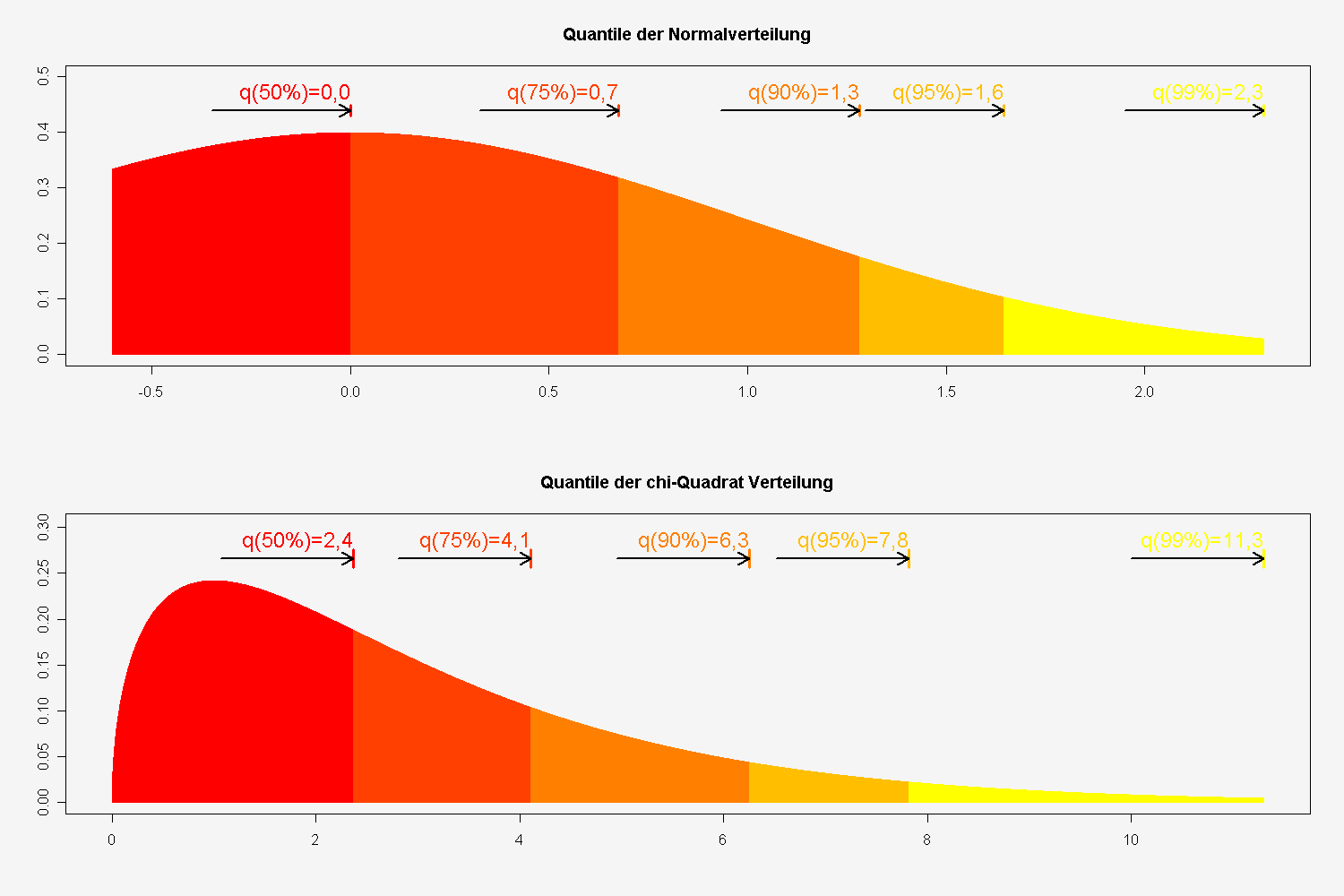
Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung
Um zu testen, ob vorliegende Daten normalverteilt sind, können unter Anderem der Kolmogorov-Smirnov-Test und der Shapiro-Wilk-Test herangezogen werden. Mit Hilfe von Normal-Quantil-Plots (auch Quantil-Quantil-Plot oder Q-Q-Plot) ist eine einfache grafische Überprüfung auf Normalverteilung möglich.
Simulation normalverteilter Zufallsvariablen
Box-Muller-Methode
Nach der Box-Muller-Methode lässt sich eine standardnormalverteilte Zufallsvariable aus zwei gleichverteilten Zufallsvariablen , sogenannten Standardzufallszahlen, simulieren:
Polar-Methode
Die Polar-Methode von Marsaglia ist auf einem Computer noch schneller, da sie nur einen Logarithmus benutzt:
- Generiere zwei gleichverteilte Zufallsvariablen
- Berechne . Falls wiederhole 1.
Durch lineare Transformation lassen sich hieraus auch beliebige normalverteilte Zufallszahlen generieren: Ist die Zufallsvariable -verteilt, so ist aX+b schließlich -verteilt.
Zwölferregel
Der zentrale Grenzwertsatz besagt, dass sich die Verteilung der Summe unabhängiger identisch verteilter Zufallszahlen einer Normalverteilung nähert.
Ein Spezialfall ist die Zwölferregel, die sich auf die Summe von 12 Zufallszahlen aus einer Gleichverteilung auf dem Intervall [0,1] beschränkt und bereits zu passablen Verteilungen führt.
Stark ins Gewicht fällt die Forderung der Unabhängigkeit der zwölf , die von normalen Pseudozufallszahlen (LKG) nicht garantiert wird. Im Gegenteil wird vom Spektraltest meist nur die Unabhängigkeit von maximal vier bis sieben der garantiert. Für numerische Simulationen ist die Zwölferregel daher sehr bedenklich! Andere sogar leichter zu programmierende Verfahren sind unbedingt vorzuziehen!
Verwerfungsmethode
Normalverteilungen lassen sich mit der Verwerfungsmethode (s. dort) simulieren.
Inversionsmethode
Selbstverständlich lässt sich die Normalverteilung auch mit der Inversionsmethode berechnen. Da das Fehlerintegral leider nicht explizit mit elementaren Funktionen integrierbar ist, muss man auf Reihenentwicklungen der inversen Funktion für einen Startwert ( weiter unten) und anschließende Korrektur mit dem Newtonverfahren zurückgreifen. Dazu werden erf(x) und erfc(x) benötigt, die ihrerseits mit Reihenentwicklungen und Kettenbruchentwicklungen berechnet werden können - insgesamt ein relativ hoher Aufwand. Die notwendigen Entwicklungen sind in der Literatur zu finden William B. Jones, W. J. Thron; Continued Fractions: Analytic Theory and Applications; Addison Wesley, 1980.
Entwicklung des inversen Fehlerintegrals (wegen des Pols nur als Startwert für das Newtonverfahren verwendbar):
mit den Koeffizienten
"Offensichtlich" ist das gefährlichste Wort in der Mathematik.
Eric Temple Bell
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Normalverteilung
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе