Betaverteilung

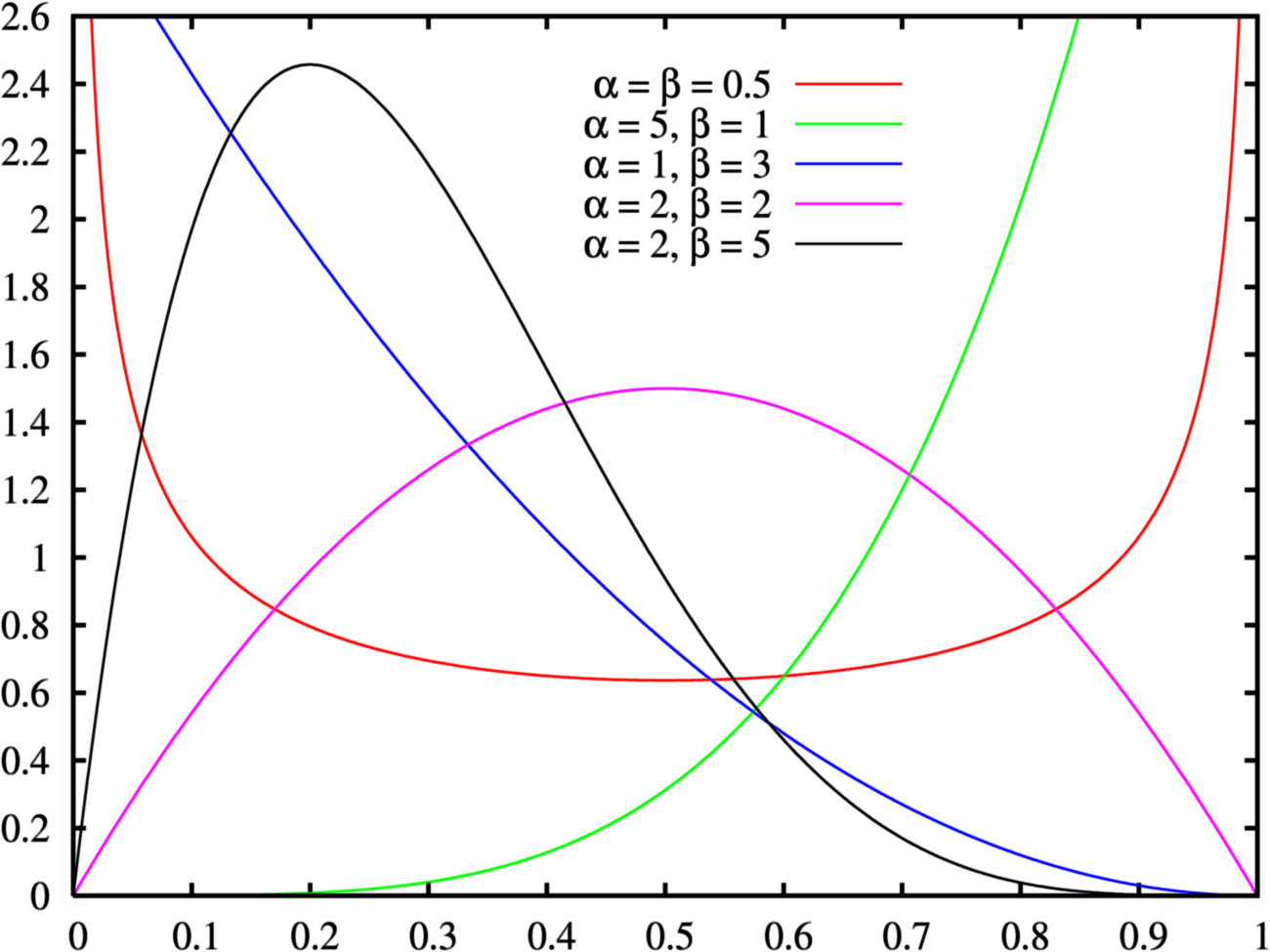
Beta_distribution_pdf.png
Betaverteilung für verschiedene Parameterwerte
Die Betaverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung über dem Intervall [0,1][0,1].

Definition

Die Beta-Verteilung ist definiert durch die Wahrscheinlichkeitsdichte
f(x)=1B(p,q)xp−1(1−x)q−1 f(x)=\dfrac{1}{ {B(p,q)}}x^{p-1}(1-x)^{q-1}\,
Außerhalb des Intervalls [0,1][0,1] wird sie durch f(x)=0f(x)=0 fortgesetzt. Sie besitzt die Parameter pp und qq. Um ihre Normierbarkeit zu garantieren, wird p,q>0p,q > 0 gefordert.
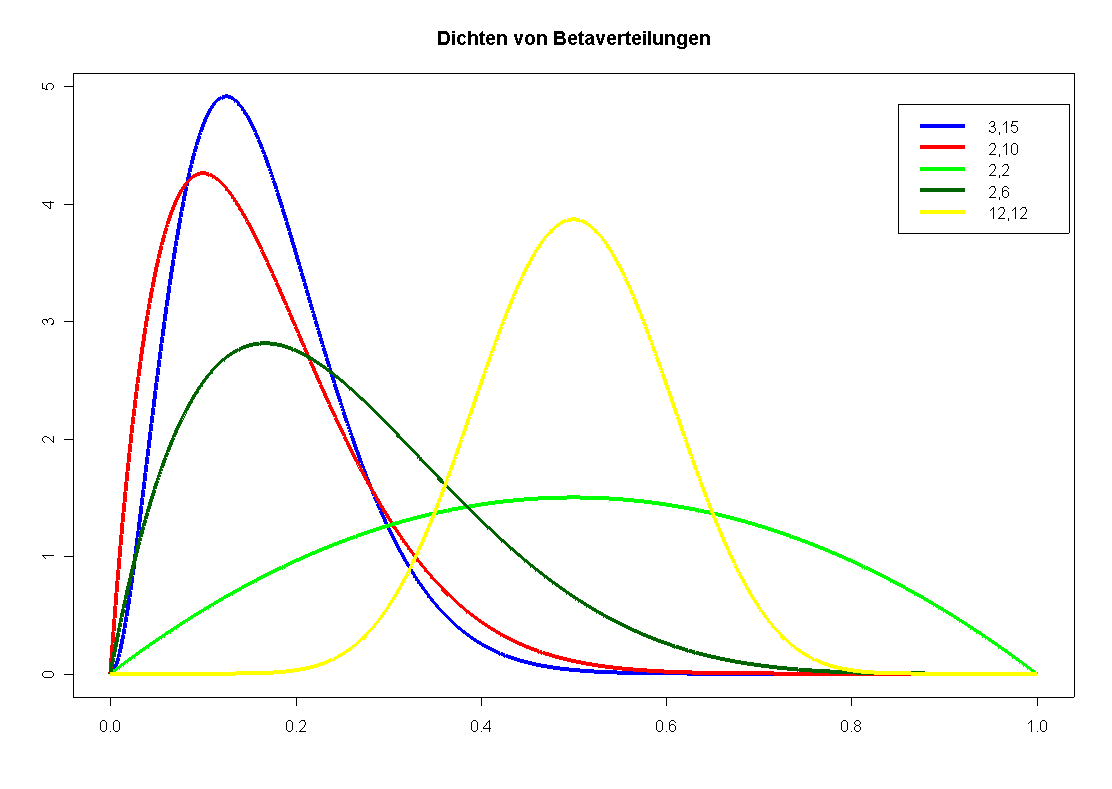
516_Beta-distribution.png
Dichten verschiedener beta-verteilter Zufallsgrößen
Der Vorfaktor 1/B(p,q)1/B(p,q) dient der korrekten Normierung. Der Ausdruck
B(p,q)=Γ(p)Γ(q)Γ(p+q)B(p,q)=\dfrac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}=∫01up−1(1−u)q−1 du=\int\limits_0^1 u^{p-1} (1-u)^{q-1} \, du
steht für Betafunktion, nach der die Verteilung benannt ist. Dabei ist Γ(x)\Gamma(x) die Gammafunktion.

Eigenschaften

Maximum

Die Dichtefunktion ff besitzt ihr Maximum an der Stelle xmax=(1+q−1p−1)−1x_{max}=\braceNT{1+\dfrac{q-1}{p-1}}^{-1}.

Erwartungswert

Der Erwartungswert berechnet sich zu
E⁡(X)=(pp+q)\operatorname{E}(X)=\over{p }{ p+q}.

Varianz

Die Varianz ergibt sich zu
Var⁡(X)=(pq(p+q+1)(p+q)2)\operatorname{Var}(X)=\over{pq }{ (p+q+1)(p+q)^{2}}.

Standardabweichung

Für die Standardabweichung ergibt sich
σ=pq(p+q+1)(p+q)2\sigma = \sqrt{\dfrac{pq}{(p+q+1)(p+q)^2}}.

Variationskoeffizient

Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten
VarK⁡(X)=qp(p+q+1)\operatorname{VarK}(X) = \sqrt{\dfrac{q}{p(p+q+1)}}.

Schiefe

Die Schiefe ergibt sich zu
v⁡(X)=2(q−p)p+q+1(p+q+2)pq\operatorname{v}(X) = \dfrac{2(q-p)\sqrt{p+q+1}}{(p+q+2)\sqrt{pq}}.

Symmetrie

Die Beta-Verteilung ist für p=qp=q symmetrisch um x=12x=\dfrac{1}{2} mit der Schiefe v⁡(X)=0\operatorname{v}(X)=0.

Beziehungen zu anderen Verteilungen

Beziehung zur Gammaverteilung

Wenn die Zufallsvariablen XX mit γ(a,b)\gamma(a,b)und YY mit γ(a,c)\gamma(a,c) Gamma-verteilt sind mit den Parametern a,ba, b und cc, dann ist die Größe XX+Y\dfrac{X}{X+Y} Beta-verteilt mit
B(b,c)=γ(a,b)γ(a,b)+γ(a,c)B(b,c) = \dfrac{\gamma(a,b)}{\gamma(a,b)+\gamma(a,c)}.

Beziehung zur F-Verteilung

Die Beta-Verteilung geht mit p=n/2, q=m/2p=n/2,\, q=m/2 und ganzzahligen nn und mm in die F-Verteilung über.

Beispiel

Die Betaverteilung kann aus zwei Gammaverteilungen erhalten werden: Der Quotient X=U/(U+V)X = U/(U+V) aus den stochastisch unabhängigen Zufallsvariablen UU und VV, die beide gammaverteilt sind mit den Parametern bb und pup_u bzw. pvp_v, ist betaverteilt mit den Parametern pup_u und pvp_v. UU und VV lassen sich als Chi-Quadrat-Verteilungen mit 2pu2p_u bzw. 2pv2p_v Freiheitsgraden interpretieren.
Mit Hilfe der Linearen Regression wird eine Regressionsgerade y=a+bxy = a + bx durch eine Punktwolke mit nn Wertepaaren (xi;yi)(i=1,…,n)(x_i;y_i) (i=1,\dots ,n) zweier statistischer Merkmale xx und yy gelegt, und zwar so, dass die Quadratsumme der senkrechten Abstände der yiy_i-Werte von der Geraden minimiert wird.
Die totale Streuung von y (TSS) lässt sich mit der Streuungszerlegung zerlegen in die so genannte erklärte Streuung der durch die Gerade geschätzten Werte y* (ESS) und die nichterklärte Streuung der Residuen (RSS):
TSS=ESS+RSSTSS= ESS+RSS.
Das Bestimmtheitsmaß, der Anteil der erklärten Streuung an der Gesamtstreuung
r2=ESSTSSr^{2}=\dfrac{ESS}{TSS}
beziehungsweise
r2=ESSESS+RSSr^{2}=\dfrac{ {ESS} }{ { {ESS}+{RSS}}}
ist also betaverteilt. Da das Bestimmtheitsmaß das Quadrat des Korrelationskoeffizienten von xx und yy darstellt, ist auch das Quadrat des Korrelationskoeffizienten betaverteilt.
Allerdings kann die Verteilung des Bestimmtheitsmaßes beim Modelltest der Regression durch die F-Verteilung angegeben werden, die tabelliert vorliegt.
 
 

Wie ist es möglich, daß die Mathematik, letztlich doch ein Produkt menschlichen Denkens unabhängig von der Erfahrung, den wirklichen Gegebenheiten so wunderbar entspricht?

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Betaverteilung aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Wahrscheinlichkeitstheorie