Varianz

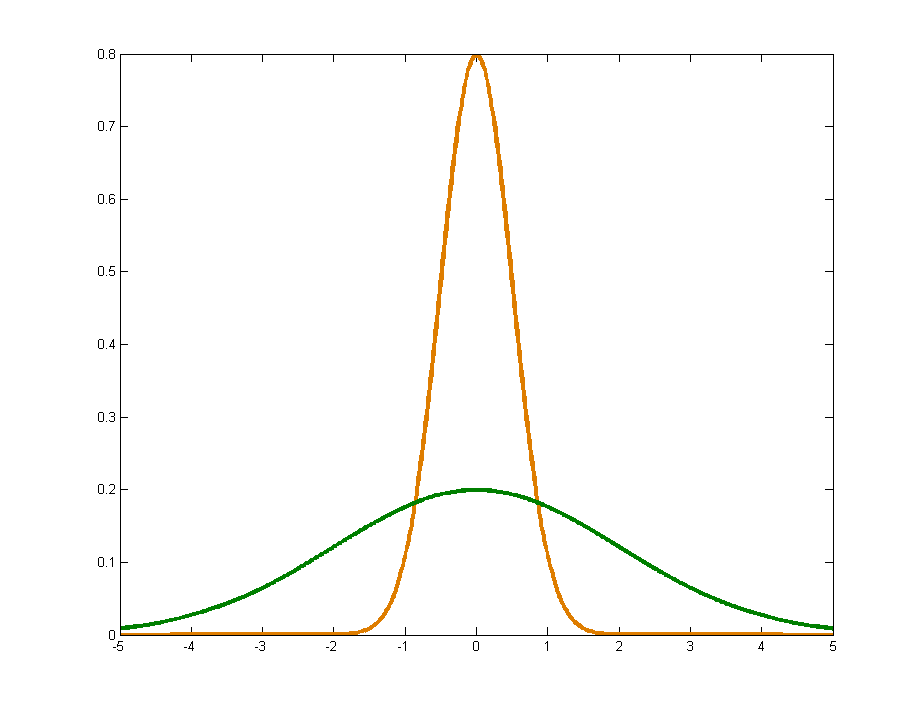
Varian.png
Zwei Normalverteilungen mit unterschiedlichen Varianzen. Die orange Kurve hat eine geringere Varianz (entsprechend der Breite) als die grüne. Die Wurzel der Varianz, die Standardabweichung, kann an den Wendepunkten ersehen werden.
Die Varianz ist ein Streuungsmaß, d.h. ein Maß für die Abweichung einer Zufallsvariable XX von ihrem Erwartungswert E⁡(X)\operatorname {E}(X). Die Varianz verallgemeinert das Konzept der Summe der quadrierten Abweichungen vom Mittelwert in einer Beobachtungsreihe. Die Varianz der Zufallsvariable XX wird üblicherweise als V⁡(X), Var⁡(X)\operatorname{V}(X),\, \operatorname{Var}(X) oder σ2\sigma^2 notiert. Ihr Nachteil für die Praxis ist, dass sie eine andere Einheit als die Daten besitzt. Dieser Nachteil kann behoben werden, indem man von der Varianz zu deren Quadratwurzel, der Standardabweichung übergeht.
In der Praxis ist die Varianz der Grundgesamtheit häufig nicht bekannt. Sie muss dann mit einem Varianzschätzer, meist mit der Stichprobenvarianz geschätzt werden.
Siehe auch: Varianzanalyse
 
 

Definition

Wenn μ=E⁡(X)\mu = \operatorname{E}(X) der Erwartungswert der quadratisch integrierbaren Zufallsvariablen XX ist, dann berechnet sich die Varianz sowohl für diskrete, wie auch stetige Zufallsvariablen zu
Var⁡(X):=V⁡(X):=E⁡((X−μ)2)\operatorname{Var}(X) := \operatorname{V}(X) := \operatorname{E}((X-\mu)^2)
Die Varianz ist also das zweite zentrale Moment einer Zufallsvariablen.
Die Varianz ist der [!Durchschnitt] der Abweichungsquadrate vom [!Durchschnitt] eines statistischen Merkmals.
Die Varianz steht in enger [!Relation] zur Standardabweichung:
σ=Var⁡(X)\sigma = \sqrt{\operatorname{Var}(X)} bzw. σ2=E⁡((X−μ)2)\sigma^2= \operatorname{E}((X-\mu)^2)

Rechenregeln

Verschiebungssatz

Var⁡(X)=E⁡((X−E⁡(X))2)=E⁡(X2)−(E⁡(X))2\operatorname{Var}(X)=\operatorname{E}\braceNT{\braceNT{X-\operatorname{E}(X)}^2}=\operatorname{E}(X^2)-\braceNT{\operatorname{E}(X)}^2

Lineare Transformation

Var⁡(aX+b)=a2Var⁡(X)\operatorname{Var}(aX+b) = a^2 \operatorname{Var}(X)
dies kann mittels des Verschiebungssatzes hergeleitet werden:
Var⁡(aX+b)=E⁡[(aX+b−E⁡(aX+b))2] \operatorname{Var}(aX+b) = \operatorname{E}[ (aX + b - \operatorname{E}(aX + b))^2 ] =E⁡[(aX+b−b−aE⁡(X))2] = \operatorname{E}[ (aX + b - b - a \operatorname{E}(X))^2 ] =E⁡[a2(X−E⁡(X))2] = \operatorname{E}[ a^2 (X - \operatorname{E}(X))^2 ] =a2E⁡[(X−E⁡(X))2] = a^2 \operatorname{E}[ (X - \operatorname{E}(X))^2 ] =a2Var⁡(X) = a^2 \operatorname{Var}(X)

Varianz von Summen von Zufallsvariablen

Var⁡(∑i=1naiXi)\operatorname{Var}\braceNT{\sum\limits_{i=1}^na_iX_i}=∑i=1nai2Var⁡(Xi)+2∑i=1n∑j=i+1naiajCov⁡(Xi,Xj) =\sum\limits_{i=1}^na_i^2\operatorname{Var}(X_i)+2\sum\limits_{i=1}^n\sum\limits_{j=i+1}^na_ia_j\operatorname{Cov}(X_i,X_j)

Charakteristische Funktion

Die Varianz lässt sich mit dem Verschiebungssatz und der charakteristischen Funktion φ \varphi der Zufallsvariablen XX darstellen als:
Var⁡(X)=φX′′(0)i2−(φX′(0)i)2\operatorname{Var}(X) = \dfrac{\varphi_X''(0)}{\mathrm{i}^{2}} - \braceNT{\dfrac{\varphi_X'(0)}{\mathrm{i}}}^{2} =φX′(0)2−φX′′(0) = \varphi_X'(0)^2 -\varphi_X''(0)

Beispiele

Diskrete Zufallsvariable

Gegeben ist eine diskrete Zufallsvariable XX mit den Wahrscheinlichkeiten
i 1 2 3
xix_{i} -1 1 2
f(xi)(x_{i}) 0,5 0,3 0,2
V⁡(X)=(−1−0,2)2⋅0,5\operatorname{V}(X) = (-1-0{,}2)^2 \cdot 0{,}5 +(1−0,2)2⋅0,3 +(1-0{,}2)^2 \cdot 0{,}3 +(2−0,2)2⋅0,2=1,56 +(2-0{,}2)^2 \cdot 0{,}2 = 1{,}56
wobei der Erwartungswert
E⁡(X)=−1⋅0,5+1⋅0,3+2⋅0,2=0,2\operatorname{E}(X) = -1 \cdot 0{,}5 + 1 \cdot 0{,}3 + 2 \cdot 0{,}2 = 0{,}2
beträgt. Mit dem Verschiebungssatz erhält man entsprechend
V⁡(X)=(−1)2⋅0,5+12⋅0,3+22⋅0,2−0,22=1,56  \operatorname{V}(X) = (-1)^2 \cdot 0{,}5 +1^2 \cdot 0{,}3 +2^2 \cdot 0{,}2 - 0{,}2^2 = 1{,}56 \ \,

Stetige Zufallsvariable

Eine stetige Zufallsvariable habe die Dichtefunktion
f(x)={1xfalls 1≤x≤e0sonst f(x) = \begin{cases} \dfrac {1}{x} & \text{falls } 1 \le x \le e \\ 0 & \text{sonst} \end{cases}
Mit dem Erwartungswert
E⁡(X)=∫1ex⋅1xdx=e−1\operatorname{E}(X) = \int\limits_1^e x \cdot \dfrac {1}{x} dx = e - 1
berechnet sich die Varianz mit Hilfe des Verschiebungssatzes als
V⁡(X)\operatorname{V}(X)=∫−∞∞x2⋅f(x)dx−(E⁡(X))2= \int\limits_{-\infty}^\infty x^2 \cdot f(x) dx - (\operatorname{E}(X))^2=∫1ex2⋅1xdx−(e−1)2 = \int\limits_1^e x^2 \cdot \dfrac {1}{x} dx - (e - 1)^2 =[x22]1e−(e−1)2= \ntxbraceL{ \dfrac{x^2}{2}} _1^e - (e - 1)^2 =e22−12−(e−1)2≈0,242 = \dfrac{e^2}{2} - \dfrac{1}{2} -(e-1)^2 \approx 0{,}242

Siehe auch

Variationskoeffizient, Kovarianz, Moment, Momenterzeugende Funktion, Charakteristische Funktion (Stochastik), Bestimmtheitsmaß, Normalverteilung

Scherzhafte Beispiele haben manchmal größere Bedeutung als ernste.

Michael Stifel

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Varianz aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Wahrscheinlichkeitstheorie