Wahrscheinlichkeitsverteilungen
In der Wahrscheinlichkeitsrechnung gibt die Wahrscheinlichkeitsverteilung an, wie sich die Wahrscheinlichkeiten auf die möglichen Zufallsergebnisse verteilen. Oftmals kann beobachtet werden, dass die Verteilung bestimmter Zufallsvariablen annähernd durch eine theoretische Verteilung dargestellt werden kann.
- Beispiel: Das Gewicht von Hähnchen einer Geflügelzucht ist meistens annähernd normalverteilt. Bei normalverteilten Daten hat diese Verteilung die Form einer Gauß'schen Glockenkurve. Meist haben diese Verteilungen bestimmte Vorzüge, sie können leicht berechnet werden, und man kann auch wahrscheinlichkeitstheoretische Folgerungen ziehen.
Dem theoretischen Begriff der Wahrscheinlichkeitsverteilung entspricht in der empirischen Statistik die Häufigkeitsverteilung, die sich aus der Analyse von Daten (Messwerten) und ihrer Streuung ergibt.
Mathematische Beschreibung
Der Begriff der Wahrscheinlichkeitsverteilung bezieht sich auf Zufallsvariablen: Unter der Verteilung der Zufallsvariable versteht man das Wahrscheinlichkeitsmaß , welches die Wahrscheinlichkeiten erfasst, mit denen die Zufallsvariable bestimmte Werte annimmt (Bildmaß von ). Wahrscheinlichkeitsmaß: Die Wahrscheinlichkeitsverteilung ergibt sich als Funktion über die einzelnen Wahrscheinlichkeiten für die einzelnen Ereignisse: Das Wahrscheinlichkeitsmaß, d. h. eine Funktion , die jedem Ereignis eine Wahrscheinlichkeit zuordnet.
Systematik 1: Diskrete und stetige Wahrscheinlichkeitsverteilungen
Es wird allgemein unterschieden zwischen diskreten und stetigen Wahrscheinlichkeitsverteilungen.
Diskrete Wahrscheinlichkeitsverteilungen
Bei diskreten Wahrscheinlichkeitsfunktionen spricht man von einer Wahrscheinlichkeitsfunktion (oder Zähldichte) bzw. . Hier hat die Zufallsvariable nur abzählbar viele Werte.
Diskrete Verteilungen sind Typen von Ziehungen vergleichbar mit einer Urne. Insbesondere sind Binomialverteilung und Hypergeometrische Verteilung von Bedeutung. Sie stellen beide Formen des Urnenmodells dar, und zwar Ziehen mit Zurücklegen und Ziehen ohne Zurücklegen. Die Poisson-Verteilung ist für den Spezialfall einer großen Anzahl von Durchführungen mit geringer Erfolgswahrscheinlichkeit eine gute Näherung an die Binomialverteilung. Die Poissonverteilung wird deshalb manchmal als die Verteilung der seltenen Ereignisse bezeichnet, siehe auch Gesetz der kleinen Zahlen.
Stetige Wahrscheinlichkeitsverteilung
Bei stetiger Wahrscheinlichkeitsverteilung spricht man von einer Dichtefunktion (oder Wahrscheinlichkeitsdichte) . Die Wahrscheinlichkeiten lassen sich als Integrale berechnen (kontinuierliche Verteilung):
- bzw.
Verteilungen auf den reellen Zahlen können allgemeiner durch die (kumulative) Verteilungsfunktion (engl. cumulative distribution function (cdf)) beschrieben werden, die angibt, mit welcher Wahrscheinlichkeit die Zufallsvariable einen Wert kleiner oder gleich annimmt:
bzw.
Die Dichtefunktion ist also die Ableitung der Verteilungsfuntion.
Wichtige stetige Wahrscheinlichkeitsverteilungen
Die meisten Wahrscheinlichkeitsverteilungen lassen sich bei großer Stichprobe zur Normalverteilung überleiten. Viele natur-, wirtschafts- und ingenieurswissenschaftliche Vorgänge lassen sich durch die Normalverteilung entweder exakt oder wenigstens in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).
Die Chi-Quadrat-Verteilung ist eine so genannte Stichprobenverteilung, die bei der Schätzung von Verteilungsparametern, beispielsweise der Varianz, Anwendung findet.
Über einem endlichen Intervall [a,b], im einfachsten Fall [0,1]:
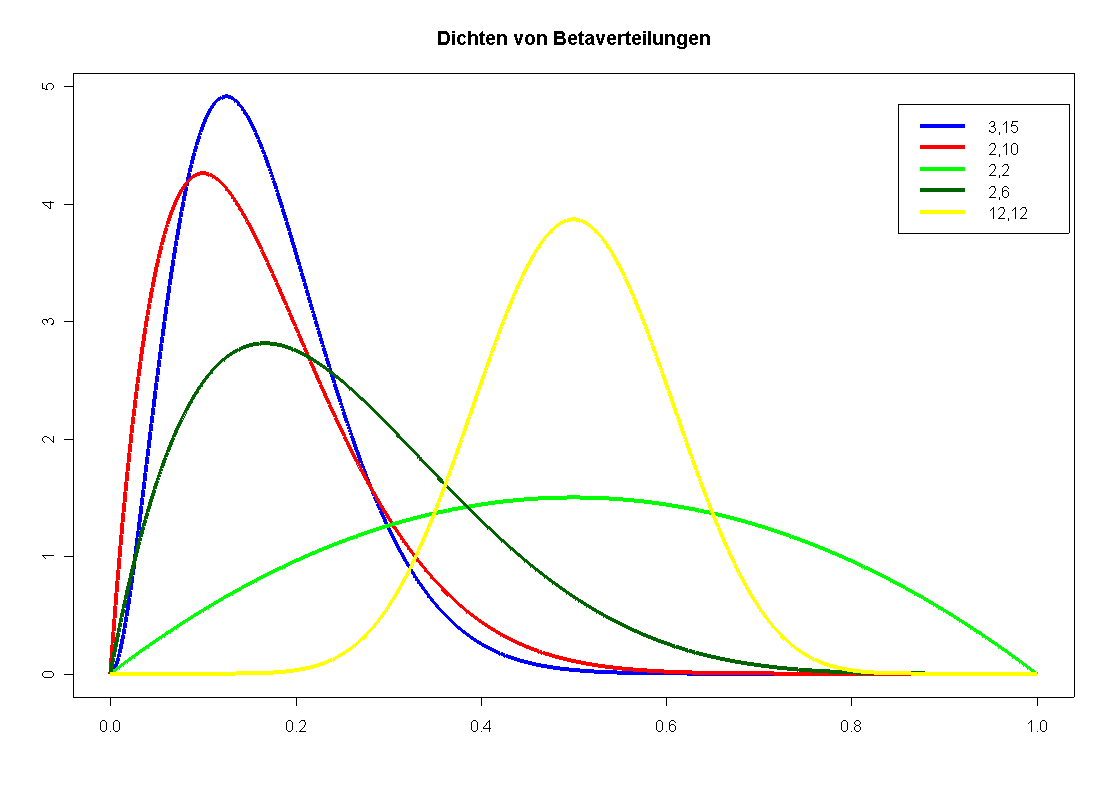
- Betaverteilung (siehe Bild)
- Dreiecksverteilung (Simpson-Verteilung)
- Stetige Gleichverteilung (Rechteckverteilung)
Über einem halbseitig unendlichen Intervall, üblicherweise als [0,] angenommen:
- -Verteilung
- Erlang-Verteilung
- Exponentialverteilung
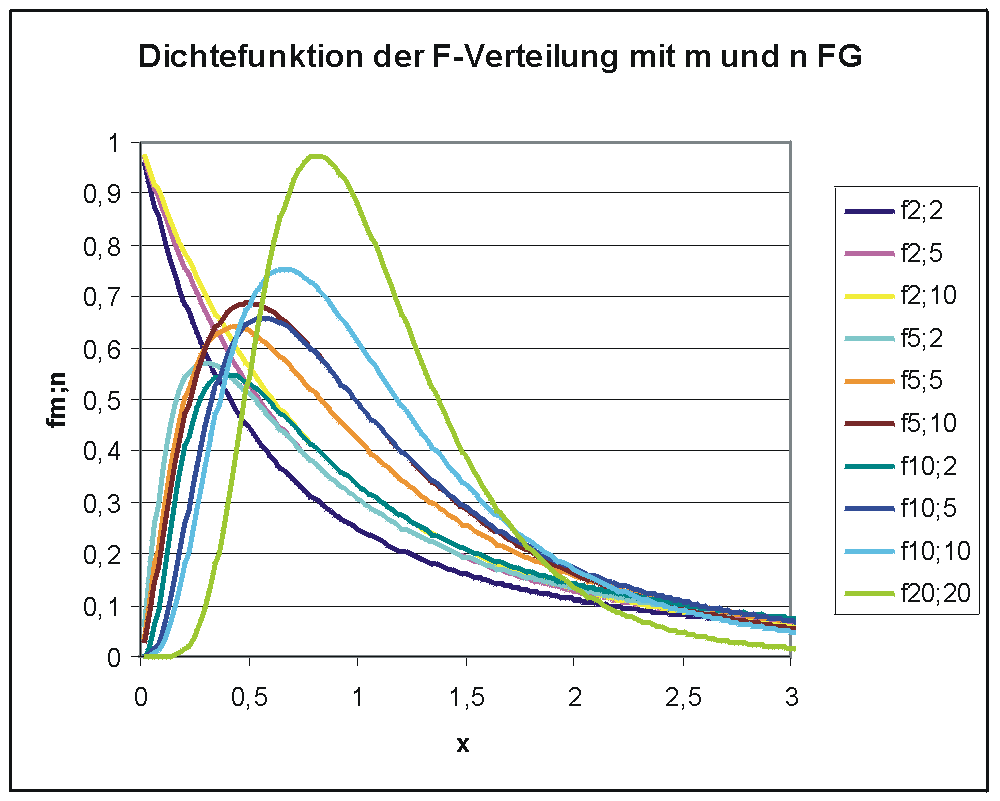
- F-Verteilung (siehe Bild)
- Gammaverteilung
- Inverse Normalverteilung (Inverse Gauß-Verteilung, Wald-Verteilung)
- Logarithmische Gammaverteilung (Log-Gammaverteilung)
- Logarithmische Normalverteilung (Log-Normalverteilung)
- Pareto-Verteilung, Verschobene Pareto-Verteilung
- Weibull-Verteilung
Über der gesamten Zahlengeraden:
- Cauchy-Verteilung (Lorentz-Verteilung)
- Extremwertverteilung
- Fisher-Tippett-Verteilung
- Fishersche z-Verteilung
- Gumbel-Verteilung
- Laplace-Verteilung (Doppelexponentialverteilung)
- Lévy-Verteilung
- Logistische Verteilung
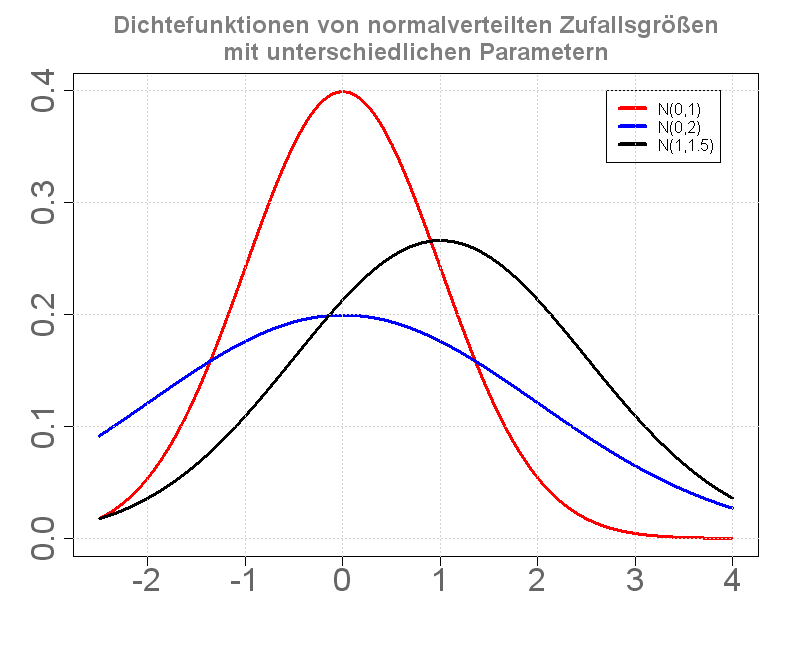
- Normalverteilung (Gauß-Verteilung, Glockenkurve, siehe Bild)
- Rayleighverteilung
- Rossi-Verteilung
- Students t-Verteilung (Student-Verteilung, t-Verteilung)
Für konvexe Kombinationen mehrerer Verteilungen siehe Mischverteilung, dessen Sonderfall
- Kontaminierte Normalverteilung
darstellt.
Systematik 2: Verteilungsklassen
Verteilungsklasse oder Verteilungsfamilie bezeichnet Verteilungen gleichen Typs. Man unterscheidet sie anhand unterschiedlicher mathematischer Eigenschaften. Man unterscheidet parametrische Klassen und nicht-parametrische Klassen. Zur Klasse der parametrischen Klassen gehört die Exponentielle Familie. Sie vereinigt:
- Normalverteilung
- Binomialverteilung
- Poissonverteilung
- Gammaverteilung
- inverse Gaußverteilung
Die Familie der Beta-Verteilungen wird "die zur Binomial-Verteilung "konjugierte" Verteilungsklasse" genannt. Die Panjer-Verteilung vereint Negative Binomialverteilung, Binomialverteilung und Poisson-Verteilung in einer Verteilungsklasse. Man sondiert auch die Verteilungsfamilie mit einen monotonen Dichtequotienten, die Dominierte Verteilungsfamilie, und Alpha-stabile Verteilungen auf Grund von unterschiedlichen Gesichtspunkten.
Literatur
- Erich Härtter: Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Vandenhoeck & Ruprecht, Göttingen 1974, ISBN 3525031149
Es gibt keinen Königsweg zur Mathematik.
Euklid
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Wahrscheinlichkeitsverteilung
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе