Binomialverteilung

Die Binomialverteilung (manchmal nicht ganz korrekt auch Bernoulli-Verteilung genannt) ist eine der wichtigsten diskreten Wahrscheinlichkeitsverteilungen.
Sie beschreibt den wahrscheinlichen Ausgang einer Folge von gleichartigen Versuchen, die jeweils nur zwei mögliche Ergebnisse haben, also die Ergebnisse von Bernoulli-Prozessen. Wenn das gewünschte Ergebnis eines Versuches die Wahrscheinlichkeit pp besitzt, und die Zahl der Versuche nn ist, dann gibt die Binomialverteilung an, mit welcher Wahrscheinlichkeit sich insgesamt kk Erfolge einstellen.
Die Binomialverteilung ist zur Beschreibung von Zufallsgrößen der folgenden Art geeignet:
  • Die Bestimmung der Anzahl einer bestimmten Eigenschaft in einer Stichprobe aus einer Menge von Elementen, wenn die Reihenfolge beim Entnehmen der Stichprobe aus der Gesamtmenge keine Rolle spielt, und die entnommenen Elemente wieder zurückgelegt werden (Ziehen mit Zurücklegen). Beispiel: Ein Korb enthält NN Bälle, davon sind MM schwarze und N−MN-M weiße. Die Wahrscheinlichkeit, einen Schwarzen zu finden, ist also p=M/Np=M/N. Es werden insgesamt nn Bälle entnommen, untersucht und wieder zurückgelegt. Dabei werden kk Schwarze identifiziert. Insgesamt gibt es NnN^{n} Möglichkeiten für die Auswahl der Bälle. In (nk)Mk(N−M)n−k\chooseNT{n}{ k}M^{k}(N-M)^{n-k} Fällen davon werden kk schwarze Bälle ausgewählt, d.h. die Wahrscheinlichkeit, unter nn Bällen kk Schwarze zu finden ist
P⁡(k)=(nk)Mk(N−M)n−kNn\operatorname{P}(k)= \chooseNT{n}{ k}\dfrac{M^{k}(N-M)^{n-k}}{N^{n}} =(nk)(MN)k(N−MN)n−k=(nk)pk(1−p)n−k = \chooseNT{n}{ k}\braceNT{\dfrac{M}{N}}^{k}\braceNT{\dfrac{N-M}{N}}^{n-k} = \chooseNT{n}{ k}p^{k}(1-p)^{n-k}.
Die Binomialverteilung ist dabei auch auf Probleme ohne Zurücklegen anwendbar. Diese Bedingung existiert in diesem Beispiel, damit die Wahrscheinlichkeit für den Erfolg sich nicht ändert.
  • Die Bestimmung der Gesamtanzahl von defekten Bauteilen, die unter identischen Bedingungen hergestellt worden sind.
  • Die Abschätzung der zufälligen Anzahl von identischen Bauteilen, die in einem Zeitintervall ausfallen, wenn sie unter gleichen Randbedingungen verwendet werden.
Die Binomialverteilung bzw. der Bernoulliversuch kann mit Hilfe des Galtonbretts veranschaulicht werden. Dabei handelt es sich um eine mechanische Apparatur, in die man eine beliebige Zahl von Kugeln werfen kann. Diese fallen dann zufällig in eines von mehreren Fächern, wobei die Aufteilung der Binomialverteilung entspricht.

Definition der Binomialverteilung

Die diskrete Wahrscheinlichkeitsverteilung
B(⋅∣p,n):Z→[0,1], k↦B(k∣p,n)=(nk)pk(1−p)n−kB(\cdot|p,n):\Bbb Z\to [0,1], \, k\mapsto B(k|p,n) = \chooseNT{n }{ k}p^k (1-p)^{n-k}
heißt die Binomialverteilung zu den Parametern nn (Anzahl der Versuche) und p∈[0,1]p\in [0,1] (Trefferwahrscheinlichkeit).
Dabei wird nur den Zahlen 0,1…n0,1\dots n eine Wahrscheinlichkeit ungleich Null zugeordnet. Die zur Trefferwahrscheinlichkeit pp komplementäre Ausfallwahrscheinlichkeit 1−p1-p wird häufig als qq abgekürzt. Nach dem binomischen Lehrsatz gilt
∑k=0n(nk)pk(1−p)n−k=1\sum\limits_{k=0}^{n} \chooseNT{n }{ k}p^k (1-p)^{n-k} = 1,
was eine notwendige Bedingung für eine Wahrscheinlichkeitsverteilung darstellt.
Eine diskrete Zufallsgröße XX heißt binomialverteilt mit den Parametern nn und pp, wenn sie die Wahrscheinlichkeiten
P⁡(X=k)=B(k∣p,n)\operatorname{P}(X=k) = B(k|p,n)
und damit die Verteilungsfunktion
FX(x)=P⁡(X≤x)=∑k=0⌊x⌋(nk)pk(1−p)n−kF_{X}(x)=\operatorname{P}(X \le x) = \sum\limits_{k=0}^{\brFloor{ x }}\chooseNT{n }{ k}p^k (1-p)^{n-k}
besitzt.

Eigenschaften der Binomialverteilung

Symmetrie

  • Die Binomialverteilung ist im Spezialfall p=0,5p = 0,5 symmetrisch und ansonsten asymmetrisch.
  • Die Binomialverteilung besitzt die Eigenschaft B(k∣p,n)=B(k∣q,n−k)B(k|p,n) = B(k|q,n-k) mit q=1−pq=1-p.

Erwartungswert und Varianz

Die Binomialverteilung besitzt den Erwartungswert npnp und die Varianz npqnpq mit q=1−pq=1-p.

Beweis

Den Erwartungswert errechnet man direkt aus der Definition E⁡(X)=∑i=1nxipi\operatorname{E}(X)=\sum\limits_{i=1}^n x_i p_i zu
E⁡(X)\operatorname{E}(X) =∑k=0nk(nk)pk(1−p)n−k=\sum\limits_{k=0}^{n} k\chooseNT{n }{ k}p^k (1-p)^{n-k}=np∑k=0nk(n−1)!(n−k)!k!pk−1(1−p)(n−1)−(k−1)= = np\sum\limits_{k=0}^{n} k\dfrac{(n-1)!}{(n-k)!k!}p^{k-1} (1-p)^{(n-1)-(k-1)}= =np∑k=1n(n−1)!(n−k)!(k−1)!pk−1(1−p)(n−1)−(k−1)=np\sum\limits_{k=1}^{n} \dfrac{(n-1)!}{(n-k)!(k-1)!}p^{k-1} (1-p)^{(n-1)-(k-1)}=np∑k=1n(n−1k−1)pk−1(1−p)(n−1)−(k−1) =np\sum\limits_{k=1}^{n} \chooseNT{n-1 }{ k-1}p^{k-1} (1-p)^{(n-1)-(k-1)} =np∑l=0n−1(n−1l)pl(1−p)(n−1)−l= np\sum_{l=0}^{n-1} \chooseNT {n-1} { l} p^{l} (1-p)^{(n-1)-l} =np∑l=0m(ml)pl(1−p)m−l=np=np\sum\limits_{l=0}^{m} \chooseNT{m }{ l} p^{l} (1-p)^{m-l} = np
oder alternativ mit der Summenregel für Erwartungswerte, wenn man berücksichtigt, dass die identischen Einzelprozesse der Bernoulli-Verteilung mit E⁡=p\operatorname{E}=p genügen zu
E⁡(X)=E⁡(X1+…+Xn)=E⁡(X1)+…+E⁡(Xn)=nE⁡(X1)=np\operatorname{E}(X)=\operatorname{E}(X_1+\ldots+X_n)=\operatorname{E}(X_1)+\ldots+\operatorname{E}(X_n)=n \operatorname{E}(X_1)=np.
Die Varianz bestimmt sich analog direkt aus dem Verschiebungssatz Var⁡(X)=E⁡(X2)−(E⁡(X))2\operatorname{Var}(X)=\operatorname{E}(X^2)-\braceNT{\operatorname{E}(X)}^2 zu
Var⁡(X)=∑k=0nk2(nk)pk(1−p)n−k−n2p2=np(1−p)=npq\operatorname{Var}(X) =\sum\limits_{k=0}^{n} k^2\chooseNT{n }{ k}p^k (1-p)^{n-k}-n^2p^2 = np(1-p)=npq
oder alternativ aus der Summenregel für die Varianz unabhängiger Zufallsvariablen, wenn man berücksichtigt, dass die identischen Einzelprozesse der Bernoulli-Verteilung mit Var⁡(X)=p(1−p)=pq\operatorname{Var}(X) = p(1-p)= pq genügen zu
Var⁡(X)=Var⁡(X1+…+Xn)=Var⁡(X1)+…+V(Xn)\operatorname{Var}(X)=\operatorname{Var}(X_1+\ldots+X_n)=\operatorname{Var}(X_1)+\ldots+V(X_n)=nVar⁡(X1)=n(p−p2)=npq =n \operatorname{Var}(X_1)=n(p-p^2)=npq.

Variationskoeffizient

Aus Erwartungswert und Varianz erhält man sofort den Variationskoeffizienten
VarK⁡(X)=1−pnp\operatorname{VarK}(X) = \sqrt{\dfrac{1-p}{np}}.

Schiefe und Wölbung

Die Schiefe ergibt sich zu
v⁡(X)=1−2pnp(1−p)\operatorname{v}(X) = \dfrac{1-2p}{\sqrt{np(1-p)}}.
Die Wölbung lässt sich ebenfalls geschlossen darstellen als
β2=1−6pqnpq\beta_2 = \dfrac{1-6pq}{npq}.

Charakteristische Funktion

Die charakteristische Funktion hat die Form
φX(s)=((1−p)+peis)n=(q+peis)n\phi_{X}(s) = ((1-p)+pe^{is})^{n} = (q+pe^{is})^{n}.

Erzeugende Funktion

Für die erzeugende Funktion erhält man
gX(s)=(ps+(1−p))ng_{X}(s) = (ps+(1-p))^{n}.

Momenterzeugende Funktion

Die momenterzeugende Funktion der Binomialverteilung ist
mX(s)=(pes+(1−p))nm_{X}(s) = (pe^{s}+(1-p))^{n}.

Summe binomialverteilter Zufallsgrößen

Für die Summe Z=X+YZ=X+Y zweier unabhängige binomialverteilte Zufallsgrößen XX und YY mit den Parametern n1, pn_1,\, p und n2, pn_2,\, p erhält man die Einzelwahrscheinlichkeiten
P⁡(Z=k)\operatorname{P}(Z=k) =∑i=0k[(n1i)pi(1−p)n1−i][(n2k−i)pk−i(1−p)n2−k+i]= \sum\limits_{i=0}^{k}\ntxbraceL{\chooseNT{n_{1}}{ i}p^{i}(1-p)^{n_{1}-i}}\ntxbraceL{\chooseNT{n_{2}}{ {k-i}}p^{k-i}(1-p)^{n_{2}-k+i}}
=(n1+n2k)pk(1−p)n1+n2−k(k=0,1,…,n1+n2)= \chooseNT{n_{1}+n_{2}}{ k}p^{k}(1-p)^{n_{1}+n_{2}-k} (k=0,1,\dots,n_{1}+n_{2})
also wieder eine binomialverteilte Zufallsgröße, jedoch mit den Parametern n1+n2n_1+n_2 und pp.
Allgemein gilt: Wenn die mm Zufallsvariablen XiX_{i} stochastisch unabhängig sind und den Binomialverteilungen B(ni,p)B(n_i,p)genügen, dann ist auch die Summe X1+X2+⋯+XmX_{1}+X_{2}+\dots +X_{m} binomialverteilt, jedoch mit den Parametern B(n1+n2+⋯+nm,p)B(n_1+n_2+\dots +n_m,p).

Beziehung zu anderen Verteilungen

Übergang zur Bernoulli-Verteilung

Die Summe von identischen Bernoulli-verteilten Zufallsgrößen genügt der Binomialverteilung.

Übergang zur Normalverteilung

Im Grenzfall n→∞n\to\infty konvergiert die Binomialverteilung gegen eine Normalverteilung, d.h. die Normalverteilung kann als brauchbare Näherung der Binomialverteilung verwendet werden, wenn der Stichprobenumfang hinreichend groß und der Anteil der gesuchten Ausprägung nicht zu klein sind.
Es gilt: μ=np\mu=np und σ2=npq\sigma^2=npq. Durch Einsetzung in die Wahrscheinlichkeitsdichte der Normalverteilung folgt:
Wpn(k)≈12πnpq ⋅exp⁡(−(k−np)22npq) W_p^n(k)\approx\dfrac{1}{\sqrt{2\pi npq}} \, \cdot\exp\braceNT{-\dfrac{ {(k-np)}^2}{ 2npq}}\,
Eine Faustregel besagt, dass diese Näherung brauchbar ist, sofern np>4np>4 und nq>4nq>4, oder auch np(1−p)≥9np(1-p)\geq 9. Je asymmetrischer die Binomialverteilung, umso größer muss nn sein, bevor die Normalverteilung eine brauchbare Näherung liefert.

Übergang zur Poisson-Verteilung

Eine asymptotisch asymmetrische Binomialverteilung, deren Erwartungswert npnp für große n→∞n\rightarrow\infty und kleine p→0p\rightarrow 0 gegen eine von nn unabhängige Konstante λ\lambda konvergiert, kann man durch die Poisson-Verteilung annähern. Der Wert λ\lambda ist dann für alle in der Grenzwertbildung betrachteten Bimonialverteilungen wie auch für die resultierende Poissonverteilung der Erwartungswert. Diese Annäherung wird auch als Poissonscher Grenzwertsatz oder als das Gesetz seltener Ereignisse bezeichnet.
P⁡(k)\operatorname{P}(k) =(nk)pk(1−p)n−k=n!(n−k)!k!(λn)k(1−λn)n−k= \chooseNT{n }{ k}p^{k}(1-p)^{n-k}=\dfrac{n!}{(n-k)!k!}\braceNT{\dfrac{\lambda}{n}}^{k}\braceNT{1-\dfrac{\lambda}{n}}^{n-k}
=n(n−1)(n−2)(n−3)…(n−k+1)nkλkk!(1−λn)n−k=\dfrac{n(n-1)(n-2)(n-3)\dots(n-k+1)}{n^{k}}\dfrac{\lambda^{k}}{k!}\braceNT{1-\dfrac{\lambda}{n}}^{n-k}
=(1−1n)(1−2n)…(1−k−1n)(1−λn)n(1−λn)−kλkk!=\braceNT{1-\dfrac{1}{n}}\braceNT{1-\dfrac{2}{n}}\dots\braceNT{1-\dfrac{k-1}{n}}\braceNT{1-\dfrac{\lambda}{n}}^{n}\braceNT{1-\dfrac{\lambda}{n}}^{-k}\dfrac{\lambda^{k}}{k!}
n→∞n\to\infty =λkk!lim⁡n→∞(1−λn)n=λkk!e−λ= \dfrac{\lambda^{k}}{k!}\lim_{n\to\infty}\braceNT{1-\dfrac{\lambda}{n}}^{n} = \dfrac{\lambda^{k}}{k!}e^{-\lambda}
Eine Faustregel besagt, dass diese Näherung brauchbar ist, sofern np≤10np\leq 10 und n>1500pn>1500p, gleichbedeutend mit n≥50n\geq 50 und p≤0,05p\leq 0,05.
Die Poisson-Verteilung ist also die Grenzverteilung der Binomialverteilung für große nn und kleine pp.

Beziehung zur negativen Binomialverteilung

Die negative Binomialverteilung hingegen beschreibt die Wahrscheinlichkeitsverteilung der Anzahl der Versuche, die erforderlich sind, um in einem Bernoulli-Prozess eine vorgegebene Anzahl von Erfolgen zu erzielen. Die Zahl der Misserfolge bis zum erstmaligen Eintritt eines Erfolgs wird durch die geometrische Verteilung beschrieben.

Beziehung zur Hypergeometrischen-Verteilung

Bei der Binomialverteilung werden die ausgewählten Stichproben wieder zur Auswahlmenge zurückgeführt, können also zu einem späteren Zeitpunkt erneut ausgewählt werden. Werden im Gegensatz dazu die Stichproben nicht zur Grundgesamtheit zurückgegeben, dann kommt die Hypergeometrische Verteilung zur Anwendung. Beide gehen bei großem Umfang NN der Grundgesamtheit und geringem Umfang nn der Stichproben ineinander über. Als Daumenwert gilt, dass für n/N≤0,05n/N\leq 0,05 die Binomialverteilung der mathematisch anspruchsvolleren Hypergeometrischen Verteilung vorgezogen werden kann, da sie nur unwesentlich voneinander abweichende Ergebnisse liefen.

Beziehung zur Multinomial-Verteilung

Die Binomialverteilung ist ein Spezialfall sowohl der Multinomialverteilung als auch der Panjer-Verteilung.

Beispiele

Symmetrische Binomialverteilung (p gleich 1/2)

Dieses Bild zeigt die Binomialverteilung für p=0,5p=0,5 und verschiedene Werte von nn als Funktion von kk:
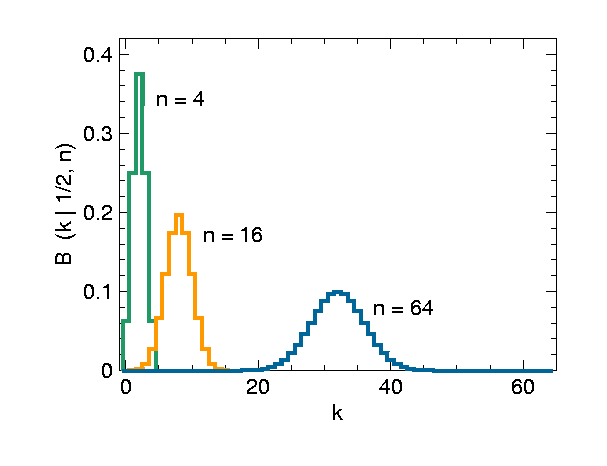
Bindis-plain.png
Diese Funktion ist spiegelsymmetrisch um den Wert k=n/2k=n/2:
B(k∣0,5,n)=B(n−k∣0,5,n)B(k|0,5,n) =B(n-k|0,5,n),
wie die folgende Auftragung zeigt:
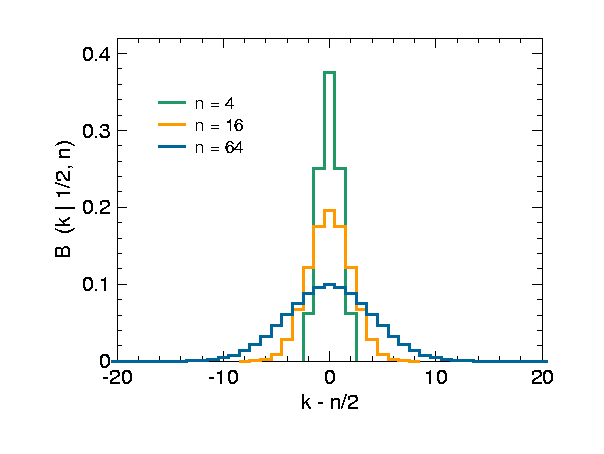
Bindis-sym.png
Die Breite der Verteilung wächst proportional zur Standardabweichung σ=(n2)\sigma = \over{\sqrt{n} }{ 2}. Der Funktionswert bei k=n/2k=n/2, also das Maximum der Kurve, sinkt proportional zu σ\sigma. Dementsprechend kann man Binomialverteilungen mit unterschiedlichem nn aufeinander skalieren, indem man die Abszisse k−n/2k-n/2 durch σ\sigma teilt und die Ordinate mit σ\sigma multipliziert:
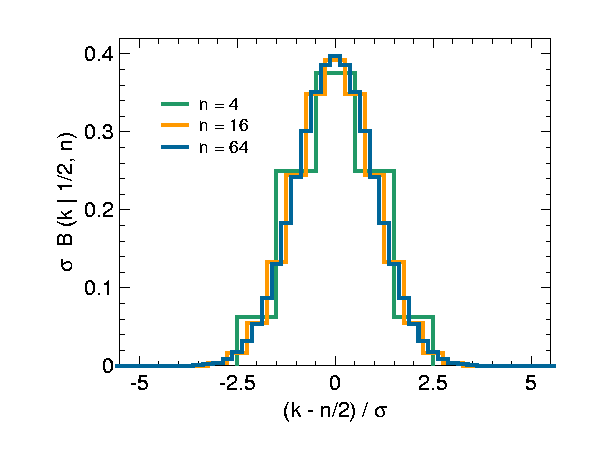
Bindis-rescaled.png
Das folgende Bild zeigt noch einmal reskalierte Binomialverteilungen, nun für andere Werte von nn und in einer Auftragung, die besser verdeutlicht, dass sämtliche Funktionswerte mit steigendem nn gegen eine gemeinsame Kurve konvergieren. Indem man die Stirling-Formel auf die Binomialkoeffizienten anwendet, erkennt man, dass diese Kurve (im Bild schwarz durchgezogen) eine Gaußsche Glockenkurve ist:
f(x)=(12π) e−x22 f(x) = \over{1 }{ \sqrt{2 \pi}} \, {\rm e}^\dfrac{-x^2}{2}.
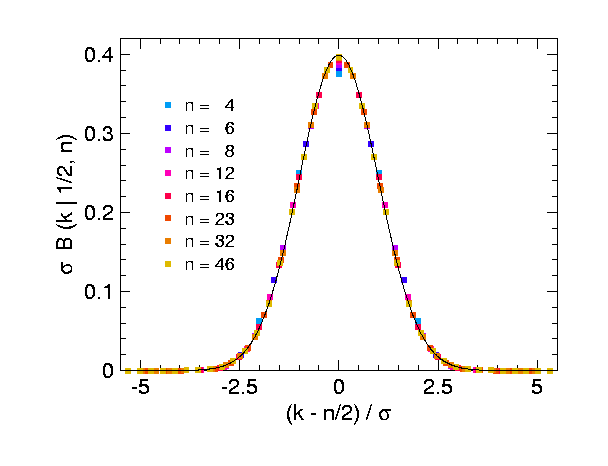
Bindis_gauss.png
Dies ist die Wahrscheinlichkeitsdichte zur Standard-Normalverteilung N(0,1)\mathcal{N}(0,1). Im zentralen Grenzwertsatz wird dieser Befund so verallgemeinert, dass auch Folgen anderer diskreter Wahrscheinlichkeitsverteilungen gegen die Normalverteilung konvergieren.
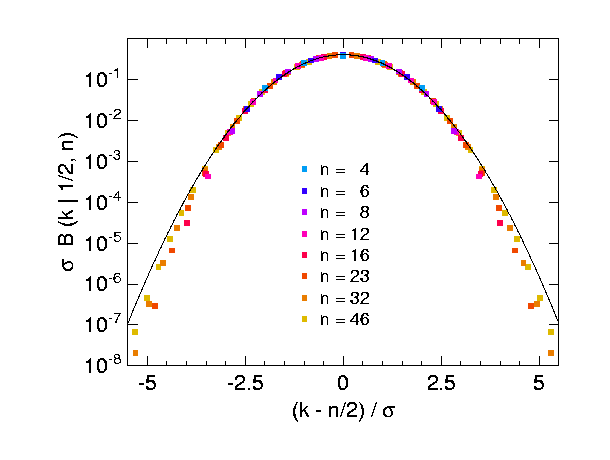
Bindis-log.png
Und hier die gleichen Daten in einer halblogarithmischen Auftragung, die sehr zu empfehlen ist, wenn man überprüfen möchte, ob auch seltene Ereignisse, die um mehrere Standardabweichungen vom Erwartungswert abweichen, einer Binomial- oder Normalverteilung folgen:
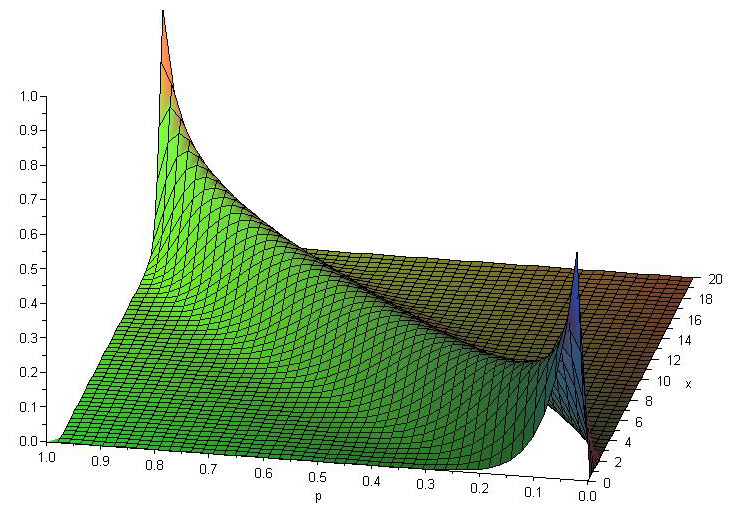
Binom3d.jpg

Allgemeiner Fall (p ∈\in [0,1])

In der Übersicht sieht man sehr gut die Auswirkung von p auf das Maximum in Bezug auf die Bedingung das ∫b(x∣p) dx=const \int\limits b(x|p) \, \mathrm{d}x = const\,

Ziehen von Kugeln

In einem Behälter befinden sich 80 Kugeln, davon sind 16 gelb. Es wird 5-mal eine Kugel entnommen und anschließend wieder zurückgelegt. Wegen des Zurücklegens ist die Wahrscheinlichkeit, eine gelbe Kugel zu ziehen, bei allen Entnahmen gleich groß: 16/80 = 1/5 = 0,2. Die Verteilung B(k|0,2; 5) gibt die Wahrscheinlichkeit dafür an, dass genau k der entnommenen Kugeln gelb sind.
B(k|0,2; 5)
k Wahrscheinlichkeit in %
0 32,768
1 40,96
2 20,48
3 5,12
4 0,64
5 0,032
Σ\Sigma 100
Erw.Wert 1
Varianz 0.8

Anzahl Personen mit Geburtstag am Wochenende

Die Wahrscheinlichkeit, dass eine Person in diesem Jahr an einem Wochenende Geburtstag hat, beträgt 2/7. In einem Raum halten sich 10 Personen auf (Darunter sind keine Zwillinge). Die Verteilung B(k|2/7; 10) gibt die Wahrscheinlichkeit dafür an, dass genau k der Anwesenden in diesem Jahr an einem Wochenende Geburtstag haben.
B(k∣2/7;10)B(k|2/7; 10)
k Wahrscheinlichkeit in %
0 3,457161303360777
1 13,828645213443108
2 24,89156138419759
3 26,55099880981076
4 18,585699166867535
5 8,921135600096417
6 2,973711866698805
7 0,6797055695311554
8 0,1019558354296733
9 0,009062740927082069
10 0,0003625096370832828
Σ\Sigma 100
Erw.Wert 2,8571428571428568
Varianz 2,040816326530612

Gemeinsamer Geburtstag im Jahr

253 Personen sind zusammen gekommen. Wie groß ist die Wahrscheinlichkeit, dass niemand der Anwesenden an einem zufällig ausgewählten Tag Geburtstag hat?
Die Wahrscheinlichkeit eines Einzelereignisses beträgt 1/365≈0,0031/365\approx 0,003, die Zahl der Versuche 253. Die direkte Berechnung der Binominalverteilung ist aufgrund der großen Fakultäten schwierig. Eine Näherung über die Poisson-Verteilung ist zulässig (n>50, p<0,05).
k(0): 0,49
k(1): 0,35
k(2): 0,12
k(3): 0,03
k(4): 0,01
Die Wahrscheinlichkeit, dass an einem ausgewählten Tag niemand Geburtstag hat, beträgt fast 50%. Die andere Hälfte der Personen hat allein Geburtstag (35%) oder teilt ihn mit einer (12%) oder zwei (3%) weiteren Personen.
Das Ergebnis sieht völlig anders aus, wenn nicht nach der Geburtstagswahrscheinlichkeit an einem Tag im Jahr gefragt wird, sondern nach der Wahrscheinlichkeit gemeinsamer Geburtstage. Statt 365 Tagen steht nur noch eine Anzahl unterschiedlicher Tage zur Verfügung, die höchstens der Zahl der Personen entspricht, siehe Geburtstagsproblem.
Anmerkung: Rechnet man mit 364/365 anstatt mit dem gerundeten Wert 0,003, so ergibt sich für k=0 (keiner der 235 Personen im Raum hat Geburtstag) eine Abweichung der Wahrscheinlichkeit um 3% ( P(k=0)=52%)

Konfidenzintervall für eine Wahrscheinlichkeit

In einer Meinungsumfrage unter n Personen geben k Personen an, die Partei A zu wählen. Bestimme ein 95% -Konfindenzintervall.
Eine Lösung des Problems ohne Rückgriff auf die Normalverteilung findet sich im Artikel Konfidenzintervall einer unbekannten Wahrscheinlichkeit.

Auslastungsmodell

Mittels folgender Formel lässt sich die Wahrscheinlichkeit dafür errechnen, dass kk von nn Personen eine Tätigkeit, die durchschnittlich mm Minuten pro Stunde dauert, gleichzeitig ausführen.
P(X=k)=(60k)⋅(m60)k⋅(1−m60)n−kP(X=k) = \chooseNT{60 }{ k}\cdot\braceNT{\dfrac{m}{60}}^k\cdot\braceNT{1-\dfrac{m}{60}}^{n-k}

Zufallszahlen

Zufallszahlen zur Binomialverteilung werden üblicherweise mit Hilfe der Inversionsmethode erzeugt.
 
 

Strukturen sind die Waffen der Mathematiker.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Binomialverteilung aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Wahrscheinlichkeitstheorie