F-Verteilung

Die F-Verteilung oder Fisher-Verteilung (nach Ronald Aylmer Fisher) ist die Wahrscheinlichkeitsverteilung einer stetigen Zufallsvariablen. Sie wird nur zum Testen verwendet, etwa bei der Varianzanalyse, um festzustellen, ob die Grundgesamtheiten zweier Stichproben die gleiche Varianz haben. Die F-Verteilung setzt sich aus den Quotienten zweier Chi-Quadrat-Verteilter Zufallsvariablen zusammen. Sie besitzt als Parameter zwei unabhängige Freiheitsgrade und bildet so eine eigene zwei-Parameter-Verteilungsfamilie.

Definition

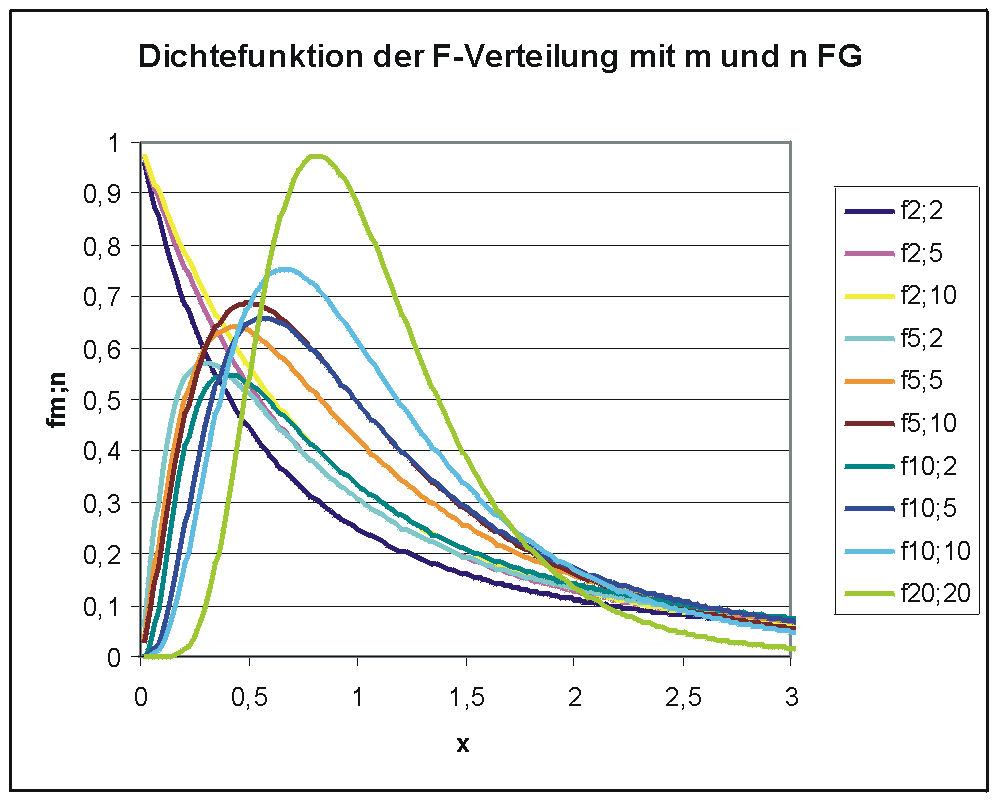
494_Fmn.png
Dichtefunktion der F-Verteilung mit ausgewählten Freiheitsgraden m und
Eine stetige Zufallsvariable genügt der F-Verteilung F(m,n)F(m,n), wenn sie die Wahrscheinlichkeitsdichte
f(x∣m;n)=mm2nn2⋅Γ(m2+n2)Γ(m2)Γ(n2)⋅xm2−1(mx+n)m+n2f(x|m;n)=m^{\dfrac{m}{2} } n^{\dfrac{n}{2}} \cdot \dfrac{\Gamma (\dfrac{m}{2} + \dfrac{n}{2})}{\Gamma (\dfrac{m}{2}) \Gamma (\dfrac{n}{2})} \cdot \dfrac{ x^{ \dfrac{m}{2} -1}}{(mx+n)^\dfrac{m+n}{2}}
besitzt. Dabei ist mit Γ(x)\Gamma(x) die Gammafunktion an der Stelle x bezeichnet.

Eigenschaften

Erwartungswert

Der Erwartungswert ist nur für n>2n>2 definiert und lautet dann
E⁡(X)=nn−2\operatorname{E}(X) = \dfrac{n}{n-2}.

Varianz

Die Varianz ist nur für n>4n>4 definiert und lautet dann
Var⁡(X)=2n2(m+n−2)m(n−2)2(n−4)\operatorname{Var}(X) = \dfrac{2 n^2 (m+n-2)}{m (n-2)^2 (n-4)}.

Verteilungsfunktion

Da die Werte der Verteilung P(X≤a)=F(a∣n;m)P(X \leq a) = F(a|n;m) nicht analytisch bestimmt werden können, müssen sie numerisch ermittelt werden. Man wird sie deshalb meistens einer F-Verteilungstabelle entnehmen. Eine komplette Tabellierung bezüglich aller Freiheitsgrade ist i.a. nicht notwendig, so dass die meisten Verteilungstabellen die Quantile bezüglich ausgewählter Freiheitsgrade und Wahrscheinlichkeiten angeben. Man macht sich hier auch die Beziehung zunutze:
F(p;m;n)=1F(1−p;n;m) ,F(p;m;n) = \dfrac{1}{F(1-p;n;m)} \, ,
wobei F(p;m;n)F(p;m;n) das pp-Quantil der F-Verteilung mit mm und nn Freiheitsgraden bedeutet.

Maximum

Für m>2m>2 nimmt ff an der Stelle
xmax=n(m−2)m(n+2)x_{max}=\dfrac{n (m-2)}{m (n+2)}
das Maximum an.

Beziehungen zu anderen Verteilungen

Beziehung zur Beta-Verteilung

Die Beta-Verteilung geht p=n/2, q=m/2p=n/2,\, q=m/2 mit ganzzahligen nn und mm geht in die F-Verteilung über.

Beziehung zur Chi-Quadrat-Verteilung

Aus den χn2\chi_n^2 und χm2\chi_m^2 Chi-Quadrat-verteilten Zufallsgrößen mit nn bzw. mm Freiheitsgraden lässt sich
F(m,n)=χm2mχn2nF(m,n)=\dfrac{\dfrac{\chi_m^2}{m}}{\dfrac{\chi_n^2}{n}}
konstruieren. Dieser Ausdruck ist F-verteilt mit mm und nn Freiheitsgraden.

Beziehung zur nichtzentralen F-Verteilung

Für unabhängige Zufallsvariablen X∼χ2(δ,m)X\sim\chi^2(\delta, m) und Y∼χ2(n)Y\sim\chi^2(n) ist
Z=XmYnZ=\dfrac{\dfrac{X}{m}}{\dfrac{Y}{n}}
verteilt nach der nichtzentralen F-Verteilung Z∼F(δ,m,n)Z\sim F(\delta,m,n) mit nichtzentralitäts-Parameter δ\delta. Dabei ist χ2(δ,m)\chi^2(\delta,m) eine Nichtzentrale Chi-Quadrat-Verteilung mit nichtzentralitäts-Parameter δ\delta und mm Freiheitsgraden. Für δ=0\delta=0 ergibt sich die zentrale F-Verteilung F(m,n)F(m,n).

Beziehung zur Normalverteilung

Wenn die identischen normalverteilten Zufallsvariablen X1(1),X2(1),…,Xn(1)X_1^{(1)}, X_2^{(1)}, \dots , X_n^{(1)} und X1(2),X2(2),…,Xn(2)X_1^{(2)}, X_2^{(2)}, \dots , X_n^{(2)} die Parameter
E⁡(Xi(1))=μ1,Var⁡(Xi(1))=σ1\operatorname{E}(X_{i}^{(1)})=\mu_{1}, \sqrt{\operatorname{Var}(X_{i}^{(1)})}=\sigma_{1}
E⁡(Xi(2))=μ2,Var⁡(Xi(2))=σ2\operatorname{E}(X_{i}^{(2)})=\mu_{2}, \sqrt{\operatorname{Var}(X_{i}^{(2)})}=\sigma_{2}
mit σ1=σ2=σ\sigma_{1}=\sigma_{2}=\sigma besitzen, dann unterliegt die Zufallsvariable
Yn1−1,n2−1:=(n2−1)∑i=1n1(Xi(1)−Xˉ(1))2(n1−1)∑j=1n2(Xi(2)−Xˉ(2))2Y_{n_{1}-1,n_{2}-1}:=\dfrac{(n_{2}-1)\sum\limits\limits_{i=1}^{n_{1}}(X_{i}^{(1)} - \bar{X}^{(1)})^{2}} {(n_{1}-1)\sum\limits\limits_{j=1}^{n_{2}}(X_{i}^{(2)}-\bar{X}^{(2)})^{2}}
einer F-Verteilung mit ((n1−1,n2−1))((n_{1}-1,n_{2}-1)) Freiheitsgraden. Dabei sind
Xˉ(1)=1n1∑i=1n1Xi(1)Xˉ(2)=1n2∑i=1n2Xi(2)\bar{X}^{(1)}=\dfrac{1}{n_{1}}\sum\limits_{i=1}^{n_{1}}X_{i}^{(1)}\quad \bar{X}^{(2)}=\dfrac{1}{n_{2}}\sum\limits_{i=1}^{n_{2}}X_{i}^{(2)}.

Literatur

Hartung, Joachim / Elpelt, Bärbel / Klösener, Karl-Heinz: Statistik, 12. Auflage, Oldenbourg 1999, S. 156 ff., ISBN 3486249843.
 
 

Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel F-Verteilung aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Wahrscheinlichkeitstheorie