Chi-Quadrat-Verteilung

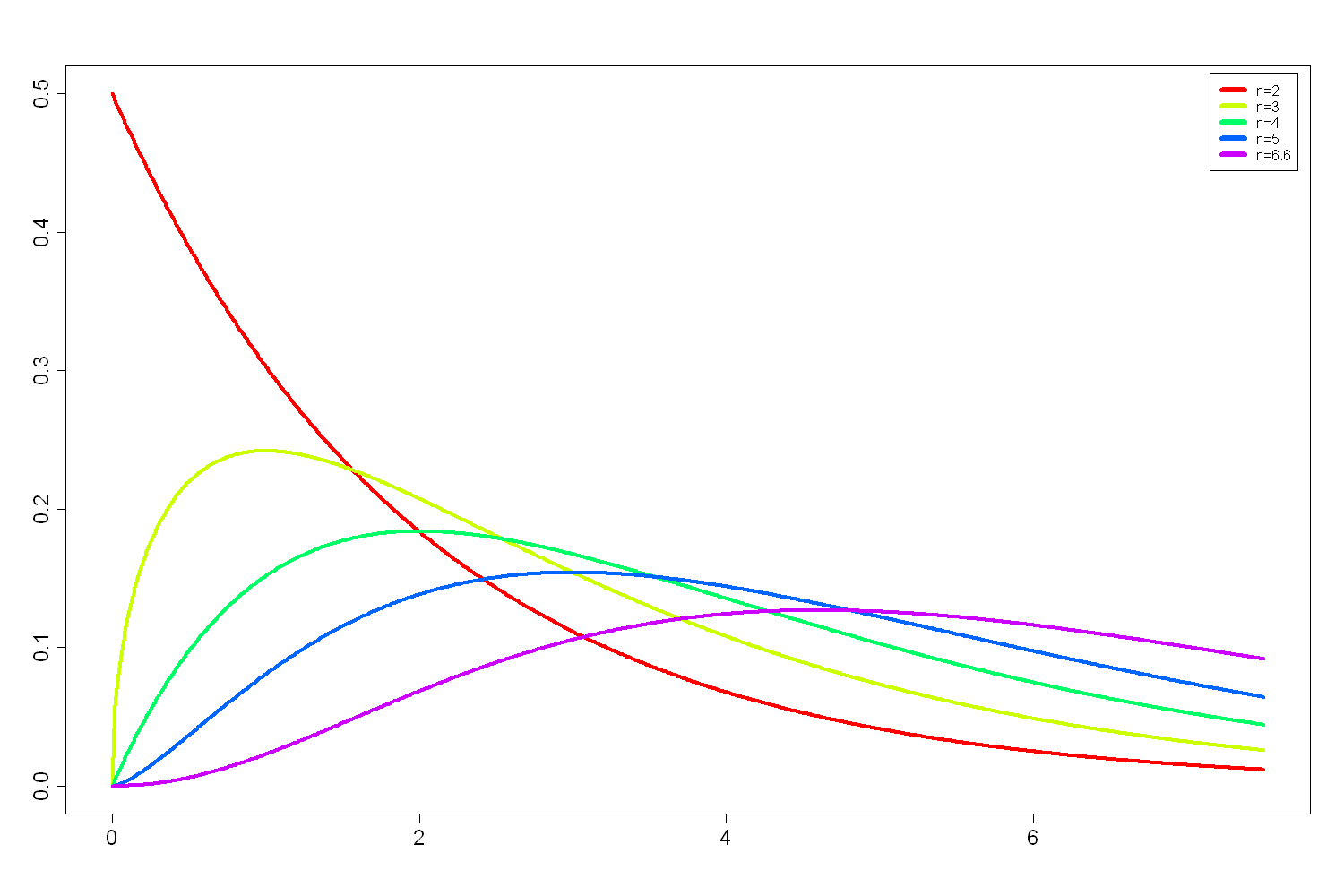
Dichten der Chi-Quadrat-Verteilung mit verschiedenen Freiheitsgraden $n$

Definition

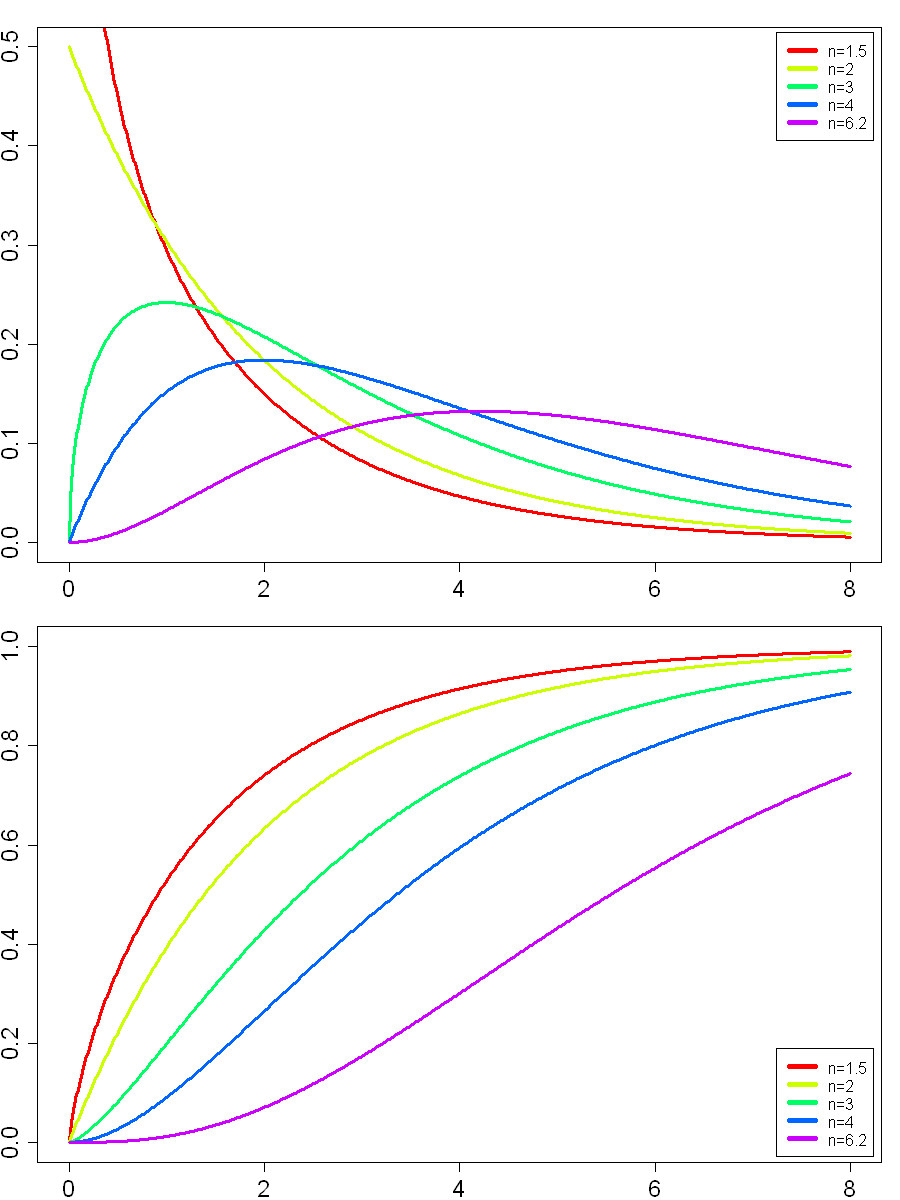
Dichte und Verteilung von mehreren Chi-quadrat Verteilten Zufallsgrößen

$\chi_n^2 = Z_1^2 + \ldots + Z_n^2$

$Z_k\sim \mathcal{N}(0,1)$ für $k = 1, \dots, n$.

$\chi^2\sim\chi^2_n\, \,$

Dichte

$f_{n}(x) = \begin{cases}\displaystyle \dfrac{x^{\dfrac{n}{2}-1}e^{ -\dfrac{x}{2}}}{2^{\dfrac{n}{2}}\Gamma\braceNT{\dfrac{n}{2}}} & x>0 \\ 0 & x\leq 0 \end{cases}$

Verteilungsfunktion

$F_n(x)= P\braceNT{\dfrac{n}{2},\dfrac{x}{2}}$

Eigenschaften

Erwartungswert

$\operatorname{E}(X) = n$.

Varianz

$\operatorname{Var}(X) = 2n$.

Modus

Schiefe

$\operatorname{v}(X) = \dfrac{2 \sqrt{2}}{\sqrt{n}}$.

Summe $\chi$²-verteilter Zufallsvariablen

$\sum\limits_{i=1}^n X_i \sim\chi^2(\sum\limits_{i=1}^n \nu_i)$

Nichtzentrale Chi-Quadrat-Verteilung

$\sum\limits_{i=1}^n {Z_i}^2\sim \chi^2(n,\lambda)$ mit $\lambda=\sum\limits_{i=1}^n {\mu_i}^2$.

$\chi^2(n+2 \, j)=\chi^2(n,\lambda)$,

$f(x)=\dfrac{\exp{\ntxbraceL{-\dfrac{1}{2}(x+\lambda)}}}{2^{\dfrac{n}{2}}} \, \sum\limits_{j=0}^\infty \dfrac{x^{\dfrac{n}{2}+j-1}\lambda^j}{2^{2j} \, \Gamma\braceNT{\dfrac{n}{2}+j} \, j!}$ für $x\ge 0,\, f(x)=0$ für $x< 0$.

Darstellung durch modifizierte Bessel-Funktion

$f(x)=\dfrac{\exp{\ntxbraceL{-\dfrac{1}{2}(x+\lambda)}} x^{\dfrac{1}{2}(n-1)} \sqrt{\lambda}}{2(\lambda x)^{\dfrac{n}{4}}} \, I_{\dfrac{n}{2}-1}\braceNT{\sqrt{\lambda x}}$ für $x\ge 0$.

Beziehung zu anderen Verteilungen

Beziehung zur Gammaverteilung

$X \sim \Gamma\braceNT{\dfrac{n}{2},\dfrac{1}{2}}$.

Beziehung zur Normalverteilung

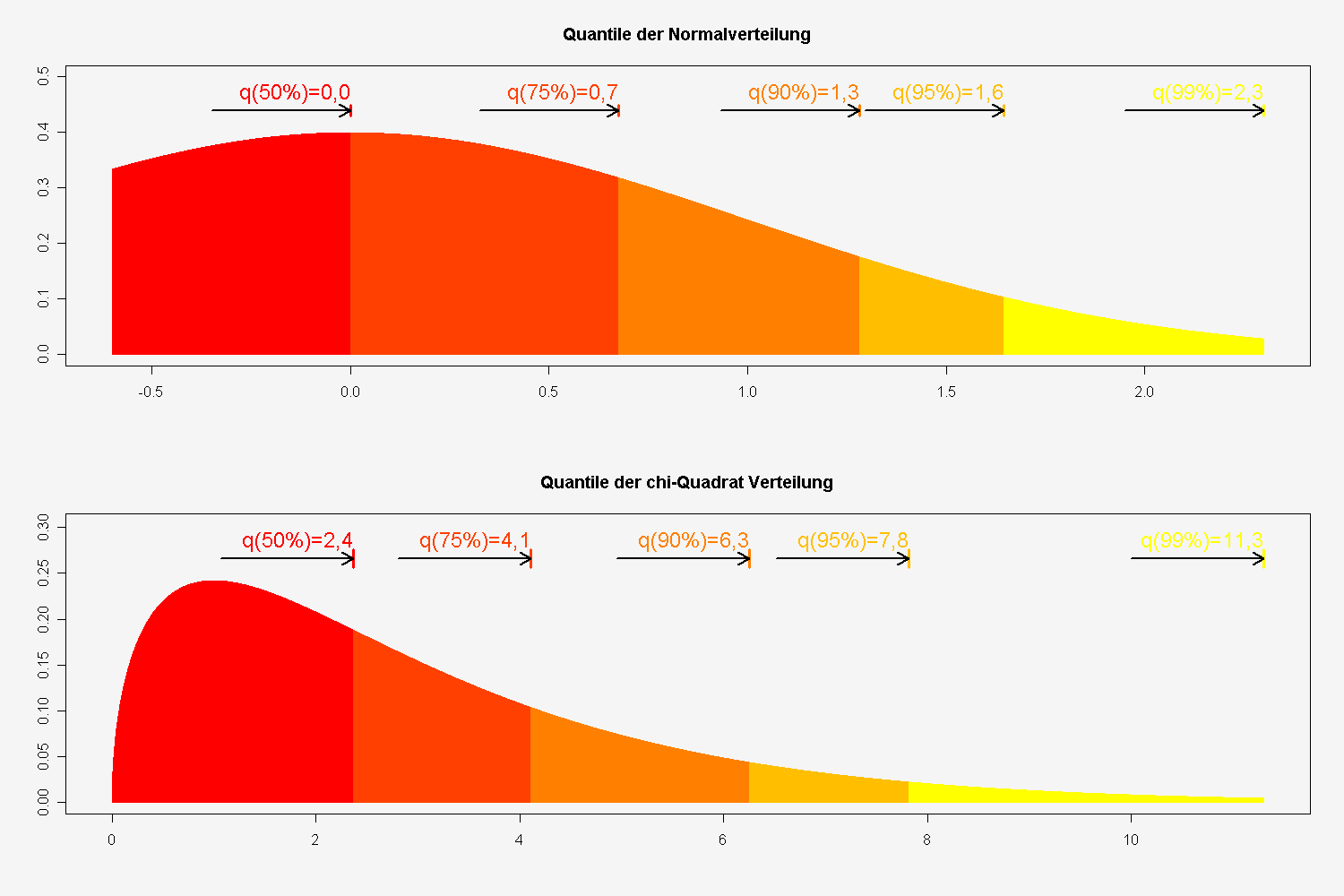
Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung

• Die Summe $X_n=Z_1^2 + \ldots + Z_n^2$ von $n$ unabhängigen quadrierten standardnormalverteilten Zufallsvariablen $Z_i\sim \mathcal{N}(0,1)$ $(i=1,\ldots,n)$ genügt einer Chi-Quadrat-Verteilung $X_n\sim\chi^2_n$ mit $n$ Freiheitsgraden.
• Für $n \geq 30$ ist $Y = \sqrt{2X} - \sqrt{2n-1}$ näherungsweise standardnormalverteilt.
• Für $n>100$ ist die Zufallsvariable $X$ näherungsweise normalverteilt mit $\mathcal{N}\braceNT{ \mu = n, \sigma=\sqrt{2n}}$, wobei $\mu$ bzw. $\sigma$ Erwartungswert und Standardabweichung darstellen.

Beziehung zur Exponentialverteilung

Beziehung zur Erlang-Verteilung

Beziehung zur F-Verteilung

$F_{m,n}=\dfrac{Y_{1m}/m}{Y_{2n}/n}$

Beziehung zur stetigen Gleichverteilung

$\chi_n^2 = -\dfrac 12\ln{\braceNT{\prod\limits_{i=1}^m u_i}}=-\dfrac 12\sum\limits_{i=1}^m \ln(u_i)$,

$\chi_n^2 = \chi_{n-1}^2 + \ntxbraceL{\mathcal{N}(0,1)}^{2}$

Literatur

Wer die erhabene Weisheit der Mathematik tadelt, nährt sich von Verwirrung.

Leonardo da Vinci

Wahrscheinlichkeitstheorie

• Zufallsvariablen
• Wahrscheinlichkeitsverteilungen
  • Gleichverteilung
  • Normalverteilung
  • Inverse Normalverteilung
  • Exponentialverteilung
  • Binomialverteilung
  • Poisson-Verteilung
  • Gammaverteilung
  • Chi-Quadrat-Verteilung
  • Erlang-Verteilung
  • F-Verteilung
  • Betaverteilung
• Monte-Carlo-Methode