Erwartungswert

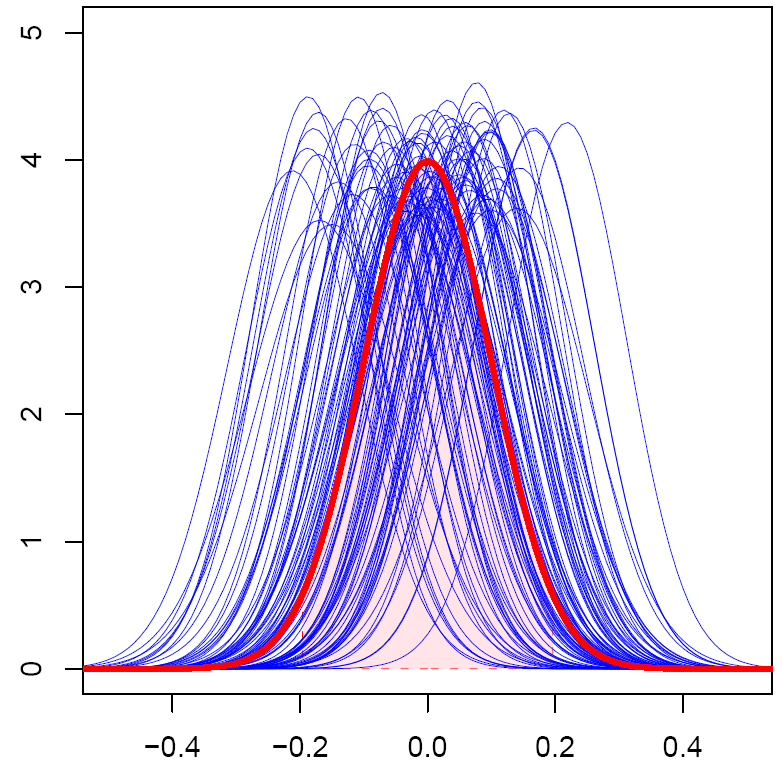
Erwartungswert.png
Errechnung des Erwartungswerts durch Mittelung wiederholter Zufallsexperimente
Der Erwartungswert (selten und doppeldeutig Mittelwert) ist ein Begriff der schließenden Statistik. Der Erwartungswert (E⁡(X)\operatorname{E}(X) oder μ\mu) einer Zufallsvariablen (X)(X) ist jener Wert, der sich (in der Regel) bei oftmaligem Wiederholen des zugrunde liegenden Experiments als Mittelwert der Ergebnisse ergibt. Er bestimmt die Lokalisation (Lage) einer Verteilung. Er ist vergleichbar mit dem empirischen arithmetischen Mittel einer Häufigkeitsverteilung in der deskriptiven Statistik. Das Gesetz der großen Zahlen sichert in vielen Fällen zu, dass der Stichprobenmittelwert bei wachsender Stichprobengröße gegen den Erwartungswert konvergiert.
Ein Erwartungswert muss kein mögliches Ergebnis des zugrunde liegenden Zufallsexperiments sein. Insbesondere kann der Erwartungswert die Werte ±∞\pm \infty annehmen.

Definitionen

Allgemein wird der Erwartungswert als das Integral bezüglich des Wahrscheinlichkeitsmaßes definiert: Ist XX eine PP-integrierbare oder quasiintegrierbare Zufallsvariable von einem Wahrscheinlichkeitsraum (Ω,Σ,P)(\Omega,\Sigma,P) nach (R‾,B)(\overline{\R},\mathcal{B}), wobei B\mathcal{B} die Borelsche σ\sigma-Algebra über R‾:=R∪{−∞,∞}\overline{\R}:=\R\cup\{-\infty,\infty\} ist, so definiert man
E⁡(X)=∫ΩX dP=∫ΩX(ω)P(dω) \operatorname{E}(X) = \int\limits_\Omega X \, dP = \int\limits_\Omega X(\omega)P(d\omega) \, .
Ist eine Zufallsvariable diskret oder besitzt sie eine Dichte, so existieren einfachere Formeln für den Erwartungswert, die im Folgenden aufgeführt sind.

Erwartungswert einer diskreten Zufallsvariablen

Im diskreten Fall errechnet sich der Erwartungswert als die Summe der Produkte aus den Wahrscheinlichkeiten jedes möglichen Ergebnisses des Experiments und den "Werten" dieser Ergebnisse.
Ist XX eine diskrete Zufallsvariable, die die Werte x1, x2x_1,\, x_2, ... mit den jeweiligen Wahrscheinlichkeiten p1, p2p_1,\, p_2, ... annimmt, errechnet sich der Erwartungswert E⁡(X)\operatorname{E}(X) zu:
E⁡(X)=∑ixipi=∑ixiP(X=xi)\operatorname{E}(X)=\sum\limits_{i} x_i p_i=\sum\limits_{i} x_i P(X=x_i)

Sonderfall: abzählbar unendlich viele Werte einer diskreten Zufallsvariablen

Nimmt die Zufallsvariable XX abzählbar unendlich viele Werte an, dann liegt eine unendliche Reihe vor. In diesem Fall existiert der Erwartungswert E⁡(X)\operatorname{E}(X) nur, wenn die Konvergenzbedingung
∑i=1∞∣xi∣pi<∞\sum\limits_{i=1}^\infty |x_i|p_i <\infty
erfüllt ist, d.h. die Summe für den Erwartungswert absolut konvergent ist.

Erwartungswert einer stetigen Zufallsvariablen mit Dichtefunktion

Hat eine Zufallsvariable XX eine Wahrscheinlichkeitsdichtefunktion f(x)f(x), so berechnet sich der Erwartungswert zu
E⁡(X)=∫−∞∞xf(x)dx \operatorname{E}(X)=\int\limits_{-\infty}^\infty x f(x)dx\,
Der Erwartungswert existiert nur, wenn das Integral für den Erwartungswert absolut konvergent ist, d.h. wenn das uneigentliche Integral ∫−∞∞∣x∣f(x)dx\int\limits_{-\infty}^\infty \ntxbraceI{ x } f(x)dx konvergiert.

Erwartungswert von zwei Zufallsvariablen mit gemeinsamer Dichtefunktion

Haben eine Zufallsvariable XX und eine Zufallsvariable YY eine gemeinsame Wahrscheinlichkeitsdichtefunktion f(x,y)f(x,y), so berechnet sich der Erwartungswert einer Funktion g(X,Y)g(X,Y) von XX und YY zu
E⁡(g(X,Y))=∫−∞∞∫−∞∞g(x,y)f(x,y)dxdy \operatorname{E}(g(X,Y))=\int\limits_{-\infty}^\infty \int\limits_{-\infty}^\infty g(x,y) f(x,y)dxdy\,
Der Erwartungswert existiert nur, wenn das Integral ∫−∞∞∫−∞∞∣g(x,y)∣f(x,y)dxdy\int\limits_{-\infty}^\infty \int\limits_{-\infty}^\infty \ntxbraceI{ g(x,y) } f(x,y)dxdy konvergiert.
Insbesondere ist:
E⁡(X)=∫−∞∞∫−∞∞xf(x,y)dxdy \operatorname{E}(X)=\int\limits_{-\infty}^\infty \int\limits_{-\infty}^\infty x f(x,y)dxdy\,

Beispiele

Würfeln

Das Experiment sei ein Würfelwurf. Als Zufallsvariable XX betrachten wir die gewürfelte Augenzahl, wobei jede der Zahlen 1 bis 6 mit einer Wahrscheinlichkeit von jeweils 1/6 gewürfelt wird.
E⁡(X)=∑i=16i⋅16=3,5\operatorname{E}(X)=\sum\limits_{i=1}^6 i\cdot \dfrac{1}{6} = 3{,}5
Wenn man beispielsweise 1000 Mal würfelt, d.h. das Zufallsexperiment 1000 mal wiederholt, die geworfenen Augenzahlen zusammenzählt und durch 1000 dividiert, ergibt sich mit hoher Wahrscheinlichkeit ein Wert in der Nähe von 3,5. Es ist jedoch unmöglich, diesen Wert mit einem einzigen Würfelwurf zu erzielen.

St. Petersburger Spiel

Das sogenannte St. Petersburger Spiel ist ein Spiel mit unendlichem Erwartungswert: Man werfe eine Münze, zeigt sie Kopf, erhält man 2€, zeigt sie Zahl, darf man nochmals werfen. Wirft man nun Kopf, erhält man 4€, wirft man wieder Zahl, so darf man ein drittes mal werfen, usw. Man sieht sofort, dass der Erwartungswert
E⁡(X)=2⋅12+4⋅14+⋯=1+1+⋯=∑i=1∞2i⋅12i=∞\operatorname{E}(X)= 2\cdot\dfrac{1}{2} + 4\cdot\dfrac{1}{4} + \cdots = 1 + 1 + \cdots = \sum\limits_{i=1}^\infty 2^i\cdot \dfrac{1}{2^i} = \infty
ist. Auch wenn man das Spiel noch so oft spielt, wird man am Ende nie eine Folge von Spielen haben, bei denen das Mittel aller Gewinne unendlich ist.

Rechenregeln

Der Erwartungswert ist linear, da das Integral ein linearer Operator ist. Daraus ergeben sich die folgenden zwei sehr nützlichen Regeln:

Erwartungswert der Summen von n Zufallsvariablen

Die Erwartungswerte der Summen von n Zufallsvariablen (Xi)(X_i) lässt sich berechnen als die Summe der einzelnen Erwartungswerte:
E⁡(∑i=1nXi)=∑i=1nE⁡(Xi)\operatorname{E}\braceNT{\sum\limits_{i=1}^nX_i}=\sum\limits_{i=1}^n\operatorname{E}(X_i)

Lineare Transformation

Für die Lineare Transformation Y=kX+d Y=kX + d \, gilt:
E⁡(Y)=E⁡(kX+d)=kE⁡(X)+d\operatorname{E}(Y)=\operatorname{E}(kX+d)=k\operatorname{E}(X)+d
weil
E⁡(a+bX)=∫−∞∞(a+bx)f(x) dx \operatorname{E}(a + bX) = \int\limits_{-\infty}^\infty (a + b x) f(x) \, dx =a∫−∞∞f(x) dx = a {\int\limits_{-\infty}^\infty f(x) \, dx} +b∫−∞∞x⋅f(x) dx + b {\int\limits_{-\infty}^\infty x \cdot f(x) \, dx} =a+bE⁡(X) = a + b \operatorname{E}(X)
Insbesondere:
E⁡(cX)=cE⁡(X)\operatorname{E}(cX)=c\operatorname{E}(X)

Erwartungswert des Produkts von n Zufallsvariablen

Wenn die Zufallsvariablen XiX_i stochastisch voneinander unabhängig sind, gilt:
E⁡(∏Xi)=∏ E⁡(Xi)\operatorname{E}\braceNT{\prod\limits X_{i}} = \prod\limits \, \operatorname{E}(X_{i})

Wahrscheinlichkeiten als Erwartungswerte

Wahrscheinlichkeiten von Ereignissen lassen sich auch über den Erwartungswert ausdrücken. Für jedes Ereignis AA gilt
P⁡(A)=E⁡(1A) \operatorname{P}(A) = \operatorname{E}(\mathrm1_A) \, ,
wobei 1A\mathrm1_A die Indikatorfunktion von AA ist.
Dieser Zusammenhang ist oft nützlich, etwa zum Beweis der Tschebyschow-Ungleichung.

Erwartungswerte von Funktionen von Zufallsvariablen

Wenn Y=g(X)Y=g(X) wieder eine Zufallsvariable ist, so kann man den Erwartungswert von YY wie folgt berechnen:
E⁡(Y)=∫−∞∞g(x)f(x)dx\operatorname{E}(Y)=\int\limits_{-\infty}^\infty g(x) f(x)dx.
Auch in diesem Fall existiert der Erwartungswert nur, wenn ∫−∞∞∣g(x)∣f(x)dx\int\limits_{-\infty}^\infty \ntxbraceI{ g(x) } f(x)dx konvergiert.
Bei einer diskreten Zufallsvariable verwendet man eine Summe:
E⁡(Y)=∑ig(xi)⋅pi\operatorname{E}(Y)=\sum\limits_{i} g(x_i) \cdot p_i
Ist die Summe nicht endlich, dann muss die Reihe absolut konvergieren damit der Erwartungswert existiert.

Erwartungswert von Matrizen

Ist XX eine m×nm \times n Matrix, dann ist der Erwartungswert der Matrix definiert als:
E⁡[X]=E⁡[x1,1x1,2⋯x1,nx2,1x2,2⋯x2,n⋮xm,1xm,2⋯xm,n] \operatorname{E}[X] = \operatorname{E} \begin{bmatrix} x_{1,1} & x_{1,2} & \cdots & x_{1,n} \\ x_{2,1} & x_{2,2} & \cdots & x_{2,n} \\ \vdots \\ x_{m,1} & x_{m,2} & \cdots & x_{m,n} \end{bmatrix}=[E⁡(x1,1)E⁡(x1,2)⋯E⁡(x1,n)E⁡(x2,1)E⁡(x2,2)⋯E⁡(x2,n)⋮E⁡(xm,1)E⁡(xm,2)⋯E⁡(xm,n)] = \begin{bmatrix} \operatorname{E}(x_{1,1}) & \operatorname{E}(x_{1,2}) & \cdots & \operatorname{E}(x_{1,n}) \\ \operatorname{E}(x_{2,1}) & \operatorname{E}(x_{2,2}) & \cdots & \operatorname{E}(x_{2,n}) \\ \vdots \\ \operatorname{E}(x_{m,1}) & \operatorname{E}(x_{m,2}) & \cdots & \operatorname{E}(x_{m,n}) \end{bmatrix}

Siehe auch

Literatur

  • Erich Härtter: Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Vandenhoeck & Ruprecht, Göttingen 1974, ISBN 3525031149
 
 

So kann also die Mathematik definiert werden als diejenige Wissenschaft, in der wir niemals das kennen, worüber wir sprechen, und niemals wissen, ob das, was wir sagen, wahr ist.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Erwartungswert aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Wahrscheinlichkeitstheorie