Erlang-Verteilung

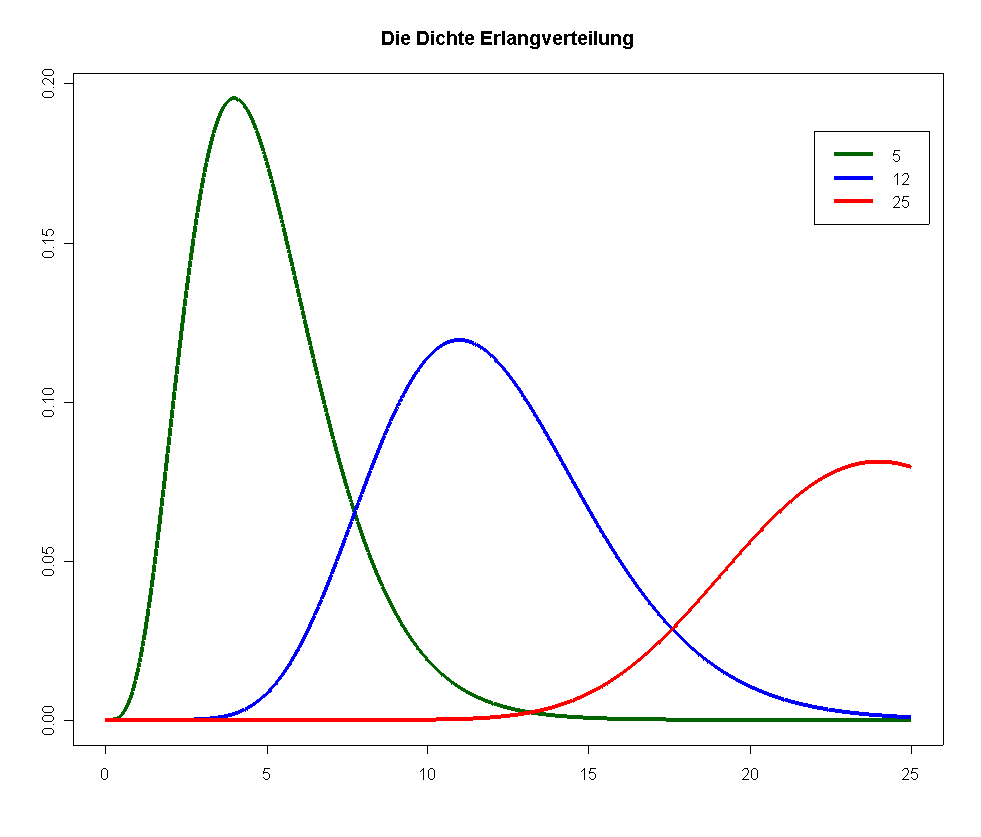
Dichte der Erlangverteilung

Definition

$f(x)=\begin{cases} \dfrac{(\lambda x)^{n-1}}{(n-1)!}\lambda e^{-\lambda x} & x\geq 0 \\ 0 & x < 0 \end{cases}$

$F(x)= \begin{cases} \dfrac{\lambda^n}{(n-1)!}\int\limits_0^x t^{n-1}e^{-\lambda t}\mathrm{d}t=\dfrac{\gamma(n, \lambda x)}{(n-1)!}=1-e^{-\lambda x} \sum\limits_{i=0}^{n-1} \dfrac{(\lambda x)^i}{i!} & x\geq 0 \\ 0 & x < 0 \end{cases}$

Eigenschaften

Erwartungswert

$\operatorname{E}(X)=\int\limits\limits_{0}^{\infty}x\dfrac{\lambda^{n}x^{n-1}}{(n-1)!} \, e^{-\lambda x}\operatorname{d}x =\dfrac{n}{\lambda}$.

Varianz

$\operatorname{Var}(X)=\int\limits\limits_{0}^{\infty}x^{2}\dfrac{\lambda^{n}x^{n-1}}{(n-1)!} \, e^{-\lambda x}\operatorname{d}x - \braceNT{\dfrac{n}{\lambda}}^{2}=\dfrac{n}{\lambda^2}$.

Beziehungen zu anderen Verteilungen

Beziehung zur Exponentialverteilung

• Die Erlang-Verteilung $\operatorname{Erl}(\lambda,n)$ ist eine Verallgemeinerung der Exponentialverteilung, denn sie geht für $n=1$ in diese über $\operatorname{Erl}(\lambda,1)=\operatorname{Exp}(\lambda)$ .
• Es seien $n$ viele, alle mit dem gleichen Parameter $\lambda$ exponentialverteilte Zufallsvariablen $Y_i\ (i = 1, \dots , n)$, die stochastisch unabhängig sind, gegeben. Dann ist die Zufallsvariable $X = Y_1 + Y_2 + \dots + Y_n$ Erlang-verteilt mit den Parametern $n$ und $\lambda (n\in\Bbb N, \lambda \geq 0)$.

Beziehung zur Poisson-Verteilung

• Für einen Poisson-Prozess wird die zufällige Anzahl der Ereignisse bis zu einem definierten Zeitpunkt mittels Poisson-Verteilung $\operatorname{Poi}(\lambda,n)$ bestimmt, die zufällige Zeit bis zum $n$-ten Ereignis ist Erlang-verteilt. Im Fall $n=1$ geht diese Erlang Verteilung in eine Exponentialverteilung über, mit der die Zeit bis zum ersten zufälligen Ereignis sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen bestimmt werden kann.
• Die Erlang-Verteilung ist die zur Poisson-Verteilung konjugierte Verteilung.

Beziehung zur stetigen Gleichverteilung

$\operatorname{Erl}(\lambda, n) \sim -\dfrac{1}{\lambda}\ln{\braceNT{\prod\limits_{i=1}^{n}x_{i}}}$.

Alles, was lediglich wahrscheinlich ist, ist wahrscheinlich falsch.

Rene Descartes

Wahrscheinlichkeitstheorie

• Zufallsvariablen
• Wahrscheinlichkeitsverteilungen
  • Gleichverteilung
  • Normalverteilung
  • Inverse Normalverteilung
  • Exponentialverteilung
  • Binomialverteilung
  • Poisson-Verteilung
  • Gammaverteilung
  • Chi-Quadrat-Verteilung
  • Erlang-Verteilung
  • F-Verteilung
  • Betaverteilung
• Monte-Carlo-Methode