Newton-Verfahren

Das Newtonsche Näherungsverfahren dient zur numerischen Lösung von nichtlinearen Gleichungen und Gleichungssystemen.

Anschauliche Beschreibung

Im Falle einer Gleichung mit einer Variablen lassen sich zu einer gegebenen stetig differenzierbaren Funktion f:R→R f: \mathbb{R} \to \mathbb{R} Näherungswerte zu Lösungen der Gleichung f(x)=0 f(x)=0, d.h. Näherungen der Nullstellen dieser Funktion finden. Die grundlegende Idee dieses Verfahrens ist, die Funktion in einem Ausgangspunkt zu linearisieren, d.h. ihre Tangente zu bestimmen, und die Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu verwenden. Die erhaltene Näherung dient als Ausgangspunkt für einen weiteren Verbesserungsschritt. Diese Iteration erfolgt bis die Änderung in der Näherungslösung eine festgesetzte Schranke unterschritten hat.
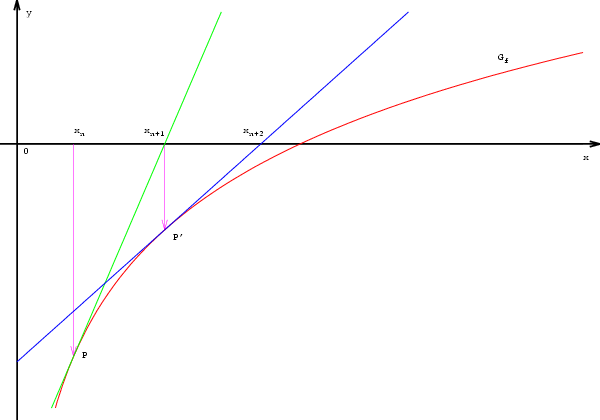
Newton.png
 
 

Newton-Verfahren für reelle Funktionen einer Veränderlichen

Sei f:R→R f: \mathbb{R} \to \mathbb{R} eine stetig differenzierbare reelle Funktion, von der wir eine Stelle xn x_n im Definitionsbereich mit "kleinem" Funktionswert kennen. Wir wollen einen Punkt xn+1 x_{n+1} nahe xn x_n finden, der eine verbesserte Näherung der Nullstelle darstellt. Dazu linearisieren wir die Funktion f f an der Stelle xn x_n , d.h. wir ersetzen sie durch ihre Tangente im Punkt P(xn ; f(xn)) P(x_n\,;\,f(x_n)) mit Anstieg f ′(xn) f\, \prime(x_n) .
Die Tangente ist durch die Funktion t(xn+h):=f(xn)+f ′(xn)h t(x_n+h):=f(x_n)+f\, \prime(x_n)h gegeben. Setzen wir h=x−xn h=x-x_n ein, so erhalten wir
t(x):=f(xn)+f ′(xn)(x−xn)t(x):=f(x_n)+f\, \prime(x_n) (x-x_n).
Wir wählen als xn+1x_{n+1} die einzige Nullstelle dieser linearen Funktion,
0=t(xn+1)=f(xn)+f ′(xn)(xn+1−xn) 0=t(x_{n+1})=f(x_n)+f\, \prime(x_n) (x_{n+1}-x_n) \quad⇒xn+1=xn−f(xn)/f′(xn) \Rightarrow\quad x_{n+1}=x_n-f(x_n)/f'(x_n) .
Wenden wir diese Konstruktion mehrfach an, so erhalten wir aus einer ersten Stelle x0 x_0 eine unendliche Folge von Stellen (xn)n∈N(x_n)_{n\in\mathbb N}, die durch die Rekursionsvorschrift
xn+1:=Nf(xn):=xn−f(xn)f ′(xn)x_{n+1}:=N_f(x_n):=x_n-\dfrac{f(x_n)}{f\, '(x_n)}
definiert ist. Diese Vorschrift wird auch als Newton-Iteration bezeichnet, die Funktion Nf N_f als Newton-Operator. Die Newton-Iteration ist ein spezieller Fall einer Fixpunktiteration, falls die Folge gegen ξ=lim⁡n→∞xn \xi=\lim_{n\to\infty} x_n\, konvergiert, so gilt ξ=Nf(ξ)=ξ−f(ξ)/f′(ξ)\xi=N_f(\xi)=\xi-f(\xi)/f'(\xi) und daher f(ξ)=0f(\xi)=0.
Die Kunst der Anwendung des Newton-Verfahrens besteht darin, geeignete Startwerte x0 x_0 zu finden. Je mehr über die Funktion f f bekannt ist, desto kleiner lässt sich die notwendige Menge von Startwerten gestalten.
Viele nichtlineare Gleichungen haben mehrere Lösungen, so hat ein Polynom n n -ten Grades bis zu n n Nullstellen. Will man alle Nullstellen in einem bestimmten Bereich D⊆R D \subseteq \R ermitteln, so muss zu jeder Nullstelle ein passender Startwert in D D gefunden werden, für den die Newton-Iteration konvergiert.

Abbruchkriterien

Mögliche Abbruchkriterien bezüglich einer Restgröße (zum Beispiel Rechner-Arithmetik) sind:
∥f(xn)∥<ε1oder∥xn+1−xn∥<ε2\| f(x_n)\|< \varepsilon_1\qquad\mathrm{oder}\qquad \| x_{n+1}-x_n\|<\varepsilon_2,
wobei ε1,ε2∈R+ \varepsilon_1,\varepsilon_2\in\mathbb{R}^+ die Qualität der "Nullstelle" bestimmt. In beiden Fällen kann es vorkommen, dass das Abbruchkriterium zu einem "schlechten" Zeitpunkt erfüllt ist.

Siehe auch

Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Newton-Verfahren aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerische Verfahren