Regula Falsi

Das Verfahren (Primitivform)

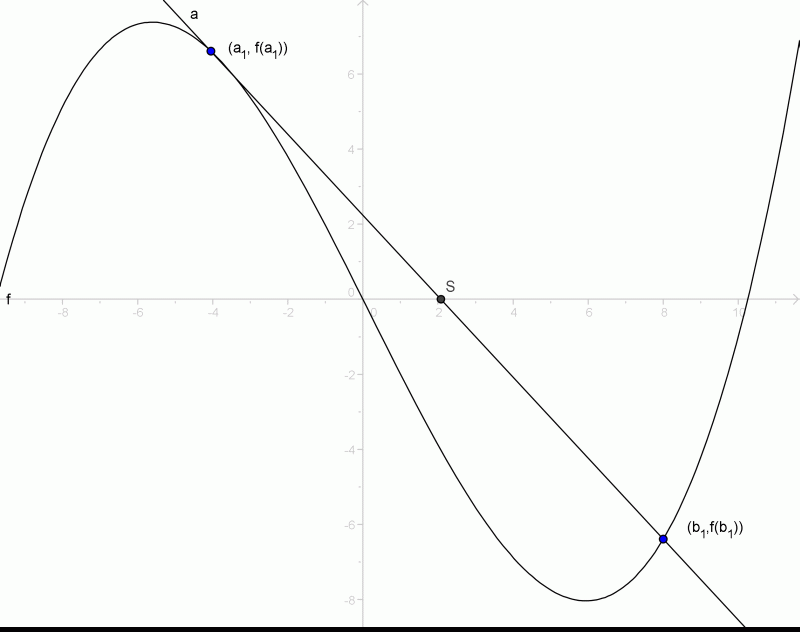
Visualisierung der Regula falsi

Iterationsvorschrift

$c_k =a_{k-1} - \dfrac{b_{k-1}-a_{k-1}}{f(b_{k-1})-f(a_{k-1})} f(a_{k-1})$

• $a_k=c_k,\ b_k=b_{k-1}$ falls $f(a_{k-1})$ und $f(c_{k})$ gleiches Vorzeichen haben
• $a_k=a_{k-1},\ b_k=c_k$ falls $f(b_{k-1})$ und $f(c_{k})$ gleiches Vorzeichen haben

Bemerkungen

• Die Berechnung des $c_{k}$ entspricht dem Anwenden des Sekantenverfahrens mit einer Iteration im $(k-1)$-ten Intervall. Im Gegensatz zum Sekantenverfahren befindet sich in diesem Intervall aber stets eine Nullstelle.
• Geometrisch kann man $c_k$ als die Nullstelle der Sekante durch $\left(a_{k-1}, f(a_{k-1})\right)$ und $\left(b_{k-1}, f(b_{k-1})\right)$ deuten.
• $c_k$ liegt natürlich immer im Intervall $\left[a_{k-1}, b_{k-1}\right]$.

Die Mathematik als Fachgebiet ist so ernst, daß man keine Gelegenheit versäumen sollte, dieses Fachgebiet unterhaltsamer zu gestalten.

Blaise Pascal

Numerische Verfahren

• Kondition
• Stabilität
• Konsistenz
• Lineare Gleichungssysteme
• Nichtlineare Gleichungssysteme
  • Sekantenverfahren
  • Regula Falsi
  • Fixpunktiteration
  • Newton-Verfahren
  • Halley-Verfahren
  • Euler-Tschebyschow-Verfahren
  • Bairstow-Verfahren
  • Weierstraß-Iteration
  • Trennkreisverfahren
• Interpolation
• Approximation
• Numerische Integration