Numerische Integration

In der numerischen Mathematik bezeichnet numerische Quadratur bzw. numerische Integration die näherungsweise Berechnung von Integralen. Oft kann man Integrale nicht geschlossen lösen, d.h. man kann keine Stammfunktion zu f(x)f(x) angeben. Deshalb versucht man, Näherungswerte zu ermitteln.
Wir bezeichnen mit
J(f)=∫abf(x)dx=Q(f)+E(f)J(f) = \int\limits_{a}^{b}f(x)dx= Q(f) + E(f)
das Integral der Funktion f(x)f(x) im Intervall [a,b][a,b]. Dies wird hier dargestellt als der Wert einer Quadraturformel Q(f)Q(f) plus dem Fehler E(f)E(f).
Dazu unterteilt man die gesuchte Fläche in senkrechte Streifen und nähert jede dieser so erhaltenen Teilflächen durch einfache geometrische Figuren (z.B. Trapez) oder einfache Funktionen (z.B. Polynome) an.
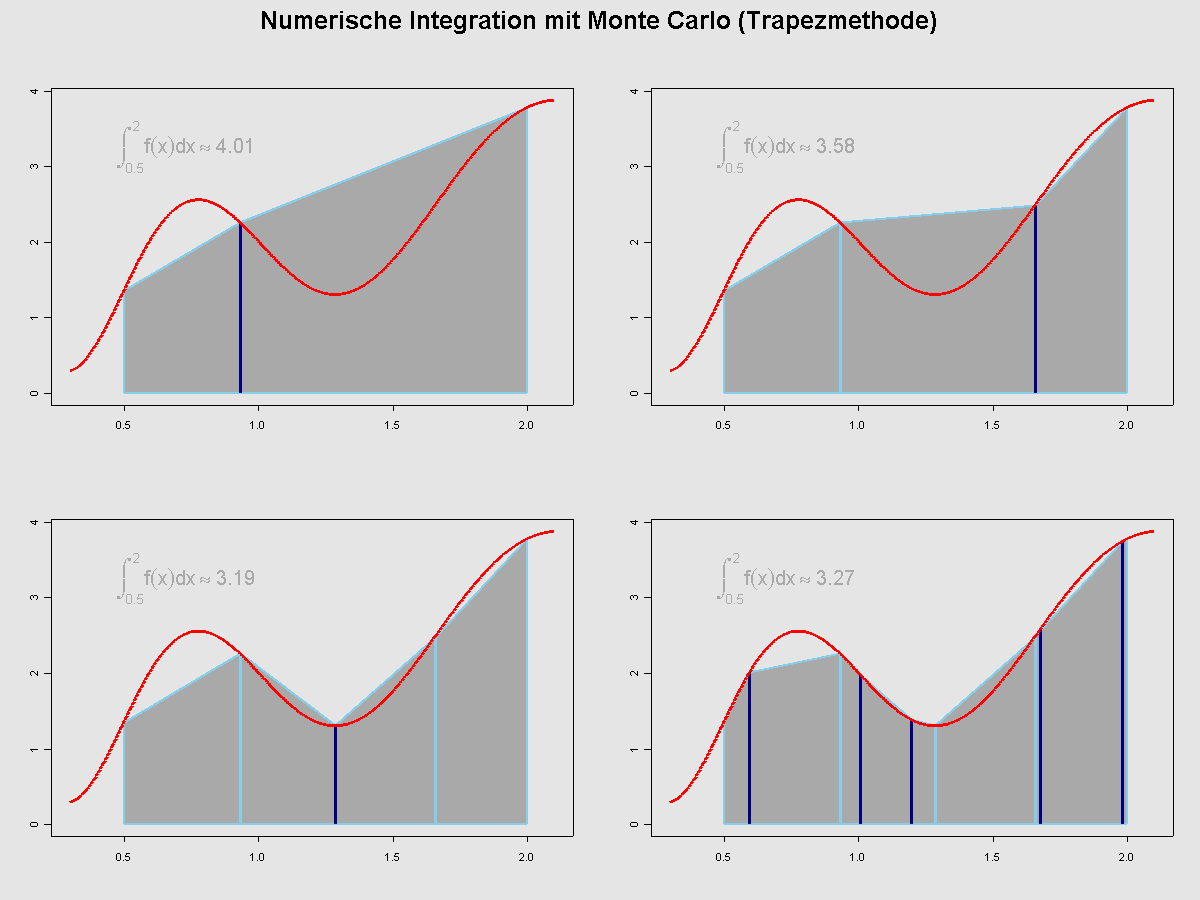
NumInt-MC.png
Numerische Integration mit dem Monte-Carlo-Algorithmus: Die Stützstellen werden zufällig gleichverteilt auf dem Integrationsintervall gewählt. Neue Stützstellen sind dunkelblau, die alten hellblau eingezeichnet. Der Wert des Integrals nähert sich 3,32 an.
Für die Flächenberechnung dieser einfachen Figuren benötigt man den Wert der Funktion f(x)f(x) an den so genannten Stützstellen x0,…xmx_0, \dots x_m. Die Summe über diese Teilflächen ergibt eine Näherung Q(f)Q(f) des Integrals. Je schmaler man die einzelnen Teilflächen wählt desto genauer wird die Näherung. Von Interesse ist dann noch die Frage, wie groß der Fehler ist, der sich durch die Näherung ergibt. Dieser Fehler wird durch das Restglied E(f)E(f) beschrieben. Um die Anzahl der Funktionsauswertungen zu minimieren, bei gleichzeitiger Möglichkeit den Fehler zu kontrollieren, verwendet man oft das Rombergsche Extrapolationsverfahren. Hierbei werden die Integralwerte von immer kleiner werdenden 'Streifen' zu einer verschwindenden Breite hin extrapoliert.
 
 

Allgemeine Quadraturformel

Mit Hilfe von Interpolationspolynomen und deren Lagrange-Darstellung kann man die folgende allgemeine Quadraturformel und das zugehörige Restglied herleiten.
Die allgemeine Quadraturformel für eine Teilfläche lautet
Q(f)=∑j=0mβj(b−a)j+1f(x0,…,xj)Q(f) = \sum\limits_{j=0}^m \beta_j(b-a)^{j+1}f(x_0,\dots ,x_j)
mit den Koeffizienten
zj=xj−ab−az_j = \dfrac{x_j -a}{b-a}
βj={1fu¨r j = 0∫01(z−z0)…(z−zj−1)dzfu¨r j=1,2,…,m\beta_j=\ntxbraceKO{\begin{matrix} 1 & \text{für }&j\text{ = 0} \\ \int\limits_0^1(z-z_0)\dots (z-z_{j-1}) dz & \text{für }&j =1,2,\dots ,m \end{matrix}}
Das Restglied beträgt
E(f)=∫ab(x−x0)…(x−xm)f(x0,  ,xm,x)dxE(f) = \int\limits_a^b(x-x_0)\dots (x-x_m)f(x_0,\, \, ,x_m,x)dx
Ist die Funktion ff im Intervall [a,b](m+1)[a,b] (m+1)-mal stetig differenzierbar ("reellwertig" wird nicht gefordert), dann lässt sich das Restglied nach oben abschätzen durch
∣E(f)∣≤((b−a)m+2(m+1)!)∫01∣(z−z0)…(z−zm)∣dz max⁡a≤x≤b∣f(m+1)(x)∣\left| E(f) \right| \le \over{(b-a)^{m+2} }{ (m+1)!}\int\limits_{0}^{1}{\left|(z-z_0)\dots (z-z_m)\right|dz}\ \max_{a\le x \le b} {\left| f^{(m+1)}(x) \right|}
Wenn noch zusätzlich für alle Stützstellen im Intervall [a,b][a,b] gilt (x−xj)≥0(x-x^j)\geq0 oder alternativ (x−xj)≤0(x-x^j)\leq 0, dann hat der Integrand keinen Vorzeichenwechsel in [a,b][a,b] und man kann zeigen:
∫01∣(z−z0)…(z−zm)∣dz=∣βm+1∣\int\limits_{0}^{1}{\left|(z-z_0)\dots (z-z_m)\right|dz} = {\left|\beta_{m+1} \right|}
Daraus folgt dann die Restgliedabschätzung
∣E(f)∣≤((b−a)m+2(m+1)!)∣βm+1∣ max⁡a≤x≤b∣f(m+1)(x)∣\left| E(f) \right| \le \over{(b-a)^{m+2} }{ (m+1)!}{\left|\beta_{m+1} \right|}\ \max_{a\le x \le b} {\left| f^{(m+1)}(x) \right|}
Ist die Funktion ff zusätzlich noch reellwertig in [a,b][a,b], dann kann man mit Hilfe des Mittelwertsatzes der Integralrechnung folgende Darstellung für das Restglied herleiten:
E(f)=((b−a)m+2(m+1)!)βm+1f(m+1)(ζ)E(f) = \over{(b-a)^{m+2} }{ (m+1)!}{\beta_{m+1}}{f^{(m+1)}(\zeta)}
mit einer Zwischenstelle ζ\zeta im Intervall [a,b][a,b].

Spezielle Quadraturformeln

Man hat nun verschiedene Möglichkeiten, die einzelnen Teilflächen durch spezielle einfachere Flächen anzunähern. Die Anwendung der allgemeinen Quadraturformeln auf diese speziellen Flächen liefert einige bekannte und wichtige spezielle Quadraturformeln.

Summierte Quadraturformeln

Um das Integral noch besser annähern zu können, unterteilt man das Intervall [a,b][a,b] in NN nebeneinanderliegende Teilintervalle [a1,b1],[a2,b2],…,[aN,bN][a_1,b_1],[a_2,b_2],\ldots,[a_N,b_N] mit  a1=a\ a_1=a;  ak+1=bk; k=1,…,N−1; bN=b\ a_{k+1}=b_k;\ k=1,\ldots,N-1;\ b_N=b.
Die Teilintervalle müssen zunächst nicht die gleiche Länge haben.
In jedem Teilintervall wendet man im Folgenden die gleiche Näherung für die einzelnen Flächen an und addiert danach die entstandenen Näherungen.
Es gilt für jede Teilfläche
∫akbkf(x)dx=Qk(f)+Ek(f)k=1,…,N\int\limits_{a_k}^{b_k}f(x)dx = Q_k(f)+E_k(f)\quad k=1,\dots ,N
Daraus folgt für das gesamte Integral
J(f)=∫abf(x)dx=∑k=1N∫akbkf(x)dx=Q(f)+E(f)J(f) = \int\limits_{a}^{b}f(x)dx = \sum\limits_{k=1}^N \int\limits_{a_k}^{b_k}f(x)dx = Q(f) + E(f)
mit
Q(f)=∑k=1NQk(f)Q(f) = \sum\limits_{k=1}^N Q_k(f)
E(f)=∑k=1NEk(f)E(f) = \sum\limits_{k=1}^N E_k(f)
Sei ff nun (m+1)(m+1)-mal stetig differenzierbar im Gesamtintervall [a,b][a,b]. Ferner sollen ab jetzt alle Teilintervalle die gleiche Länge hh haben, also
h=bk−ak=b−aNk=1,…,Nh=b_k-a_k=\dfrac{b -a}{N}\quad k=1,\dots ,N
Dann gilt für die einzelnen Restglieder (siehe oben)
∣Ek(f)∣≤(hm+2(m+1)!)∣βm+1∣ max⁡ak≤x≤bk∣f(m+1)(x)∣\left| E_k(f) \right| \le \over{h^{m+2} }{ (m+1)!}{\left|\beta_{m+1} \right|}\ \max_{a_k\le x \le b_k} {\left| f^{(m+1)}(x) \right|}
Summierung über die einzelnen Restglieder ergibt die Abschätzung für das gesamte Restglied
∣E(f)∣≤∑k=1N∣Ek(f)∣≤(b−a)(hm+1(m+1)!)∣βm+1∣max⁡ak≤x≤bk∣f(m+1)(x)∣\left| E(f)\right| \le \sum\limits_{k=1}^N \left| E_k(f) \right| \le (b-a)\over{h^{m+1} }{ (m+1)!}{\left|\beta_{m+1} \right|}\max_{a_k \le x \le b_k}{\left| f^{(m+1)}(x) \right|}
mit Nh=b−aNh = b - a.
Ist die Funktion ff zudem auf [a,b][a,b] reellwertig, dann kann man für das Restglied analog herleiten:
E(f)=(b−a)(hm+1(m+1)!)βm+1f(m+1)(ζ)E(f) = (b-a) \over{h^{m+1} }{ (m+1)!}{\beta_{m+1}}{f^{(m+1)}(\zeta)}

Siehe auch

"Offensichtlich" ist das gefährlichste Wort in der Mathematik.

Eric Temple Bell

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Numerische Integration aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerik