Keplersche Fassregel

Die Keplersche Fassregel (nach Johannes Kepler) ist eine Methode zur näherungsweisen Berechnung von Integralen. Der Magistrat der Stadt Ulm beauftragte Kepler, neue Maßeinheiten für die Stadt festzulegen. Solche praktischen Probleme des Handels hatte er schon mehrfach zuvor mathematisch gelöst. Unter anderem beschrieb er in der Nova Stereometria doliorum vinariorum von 1615 eine Methode zur Berechnung der Kapazität (genauer des Volumens) von Weinfässern mit unregelmäßigen Formen. Diese Formel liefert exakte Werte für den Pyramidenstumpf (einschließlich Pyramide), Kugel, elliptisches Paraboloid, einschaliges Hyperboloid und alle anderen Körperschichten, die sich durch ebene Körperschnitte senkrecht zu den Körperachsen erzeugen lassen. Da die Keplersche Fassregel für das Volumen von Pyramide und Tetraeder präzise Resultate ergibt, ist sie auch für Prismoide fehlerfrei anwendbar. Gute Näherungswerte liefert sie für Fässer und tonnenförmige Körper und nicht zu lange Baumstämme. Eine größere Genauigkeit kann in kritischen Fällen durch einen größeren Messaufwand erreicht werden, indem man die Messhöhe hh in n=2kn = 2k gleiche Teile zerlegt und für die entstandenen kk Schichtenpaare je einmal die Keplersche Fassregel anwendet. (siehe Simpsonsche Formel)
Simpson_rule.png
Keplersche Fassregel
Wenn man die Funktion f(x)f(x) durch eine Parabel, bestimmt durch die drei Punkte
(a;f(a))\left(a;f(a)\right), (b;f(b))\left(b;f(b)\right), (a+b2;f(a+b2))\left(\dfrac{a+b}{2};f\left(\dfrac{a+b}{2}\right)\right)
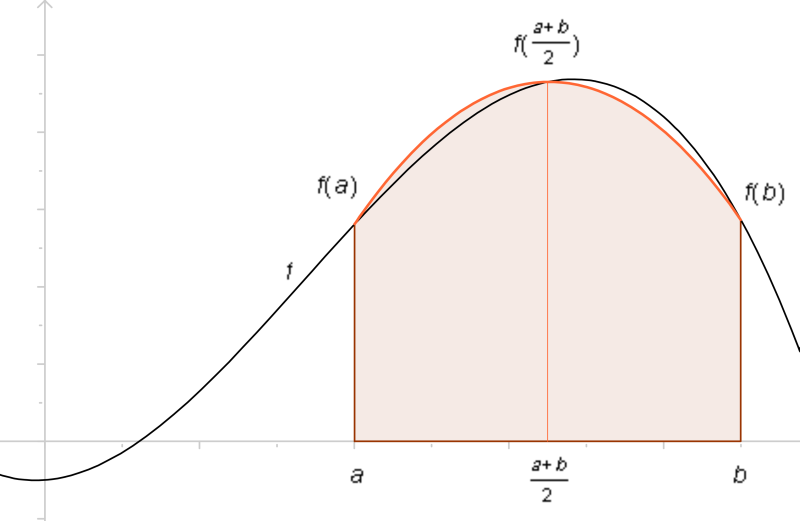
annähert, so ist die Fläche unter der Parabel durch den Ausdruck
A=b−a6⋅(f(a)+4⋅f(a+b2)+f(b))A=\dfrac{b-a}{6} \cdot \left( f(a)+4 \cdot f \left( \dfrac{a+b}{2} \right) + f(b) \right)
gegeben und berechnet eine Näherung für
I=∫abf(x) dx I = \int\limits_a^b f(x)\,\mathrm dx ,
Ist ff ein Polynom höchstens dritten Grades, so ist die Fläche sogar gleich AA.
Der Name Fassregel lässt sich durch die folgende Anwendung begründen: Zur Berechnung des Volumens eines Weinfasses sei q(x)q(x) die Querschnittsfläche quer zur Längsachse in der Entfernung xx vom Boden des Fasses; sie lässt sich durch Bestimmung des Umfanges leicht ausrechnen. Ist hh die Höhe des Fasses, so ist das Volumen gleich
V=∫0hq(x) dx V = \int\limits_0^h q(x)\,\mathrm dx\,
Die Keplersche Fassregel gibt nun
V=h6⋅(q(0)+4q(h2)+q(h))V = \dfrac{h}{6} \cdot \left(q(0) + 4q \left( \dfrac{h}{2} \right) + q(h)\right)
als Näherungswert für das Volumen eines Fasses, dessen Querschnitt an drei Stellen bekannt ist. Für bestimmte Rotationskörper wie Kegel und Kegelstumpf, Zylinder und Rotationsparaboloid gibt diese Formel das genaue Volumen an.
Ist uu der Umfang von Boden und Deckel und UU der Umfang in der Mitte des Fasses, so ergibt sich daraus die Näherungsformel:
h6⋅[2π(u2π)2+4(U2π)2π] \dfrac{h}{6}\cdot \left[ 2\pi \left( {\dfrac{u}{2\pi}} \right)^2 + 4 \left( {\dfrac{U}{2\pi}} \right)^2 \pi \right] \ = h6⋅[2π(u24π2)+4(U24π2)π] = \ \dfrac{h}{6}\cdot \left[ 2\pi \left( \dfrac{u^2}{4\pi^2} \right) + 4 \left( \dfrac{U^2}{4\pi^2} \right) \pi \right] =h12π⋅[u2+2U2]=\dfrac h{12\pi}\cdot \left[u^2 + 2U^2\right].
Der genaue Wert für eine parabolische Krümmung der Fassdauben ist
h60π⋅[3u2+4Uu+8U2]\dfrac{h}{60\pi}\cdot \left[3u^2 + 4Uu + 8 U^2 \right].

Siehe auch

 
 

Das ist ein Mittel, das Paradies nicht zu verfehlen: auf der einen Seite einen Mathematiker, auf der anderen einen Jesuiten; mit dieser Begleitung muß man seinen Weg machen, oder man macht ihn niemals.

Friedrich der Große

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Keplersche Fassregel aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerische Integration