Simpsonsche Formel

Mit der Simpsonschen Formel (auch Simpsonregel) berechnet man Näherungen zu einem Integral der Funktion f(x)f(x) im Intervall [a,b][a,b], indem man die Kurve f(x)f(x) durch eine Parabel annähert. Die Formel wurde erstmals benutzt von Evangelista Torricelli, ist aber benannt nach dem englischen Mathematiker Thomas Simpson. Sie ist die allgemeine Formulierung der Keplerschen Fassregel, die Johannes Kepler schon 200 Jahre früher aufstellte.
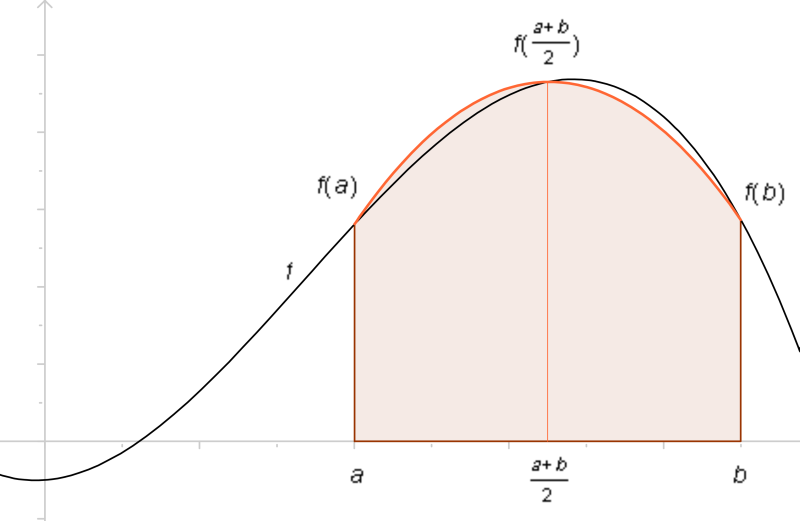
Simpson_rule.png
Simpsonsche Formel
Die Parabel wird durch die Funktionswerte an den Stellen aa, bb, (a+b)/2(a+b)/2 gelegt. Die Fläche nähert man an durch die Fläche unterhalb der Parabel.

Definition

Die Simpsonsche Formel lautet:
Q(f)=b−a6⋅(f(a)+4f(a+b2)+f(b))Q(f) = \dfrac{b-a}{6} \cdot \left( f(a)+4f \left( \dfrac{a+b}{2} \right)+f(b) \right)
Diese Formel - und auch die folgenden - kann man herleiten aus der "Allgemeinen Quadraturformel für eine Teilfläche" (siehe Numerische Quadratur).

Integraldarstellung

Damit lässt sich das Integral darstellen als
J(f)=∫abf(x)dx=Q(f)+E(f)J(f) = \int\limits_{a}^{b}f(x) \mathrm dx = Q(f) + E(f)

Restglied

Ist f(x)f(x) viermal stetig differenzierbar in [a,b][a,b], dann gilt für das Restglied E(f)E(f) folgende Abschätzung (siehe Numerische Quadratur):
∣E(f)∣≤((b−a)52880)max⁡a≤x≤b∣f(4)(x)∣\left| E(f) \right| \le \over{(b-a)^5 }{ 2880} \max_{a\le x \le b} {\left| f^{(4)}(x) \right|}
Ist f(x)f(x) zusätzlich noch reellwertig, dann gilt mit einer Zwischenstelle ζ\zeta aus [a,b][a,b] für das Restglied:
E(f)=−((b−a)52880)f(4)(ζ)E(f) = - \over{(b-a)^5 }{ 2880}{{f^{(4)}(\zeta)}}
Diese Restglieddarstellung wurde 1887 von Giuseppe Peano gefunden.

Summierte Simpsonsche Formel

Um das Integral noch besser annähern zu können, unterteilt man das Intervall [a,b][a,b] in NN nebeneinanderliegende, gleich große Teilintervalle der Länge hh. In jedem Teilintervall wendet man die Simpsonsche Formel für die einzelnen Teilflächen an und addiert danach die entstandenen Näherungen. Damit erhält man die summierte oder zusammengesetzte Simpsonsche Formel:
Q(f)=(h3)⋅((12)f(x0)+∑k=1N−1f(xk)+2∑k=1Nf(xk−1+xk2)+(12)f(xN))Q(f)=\over{h }{ 3} \cdot \left( \over{1}{ 2} f(x_0)+\sum\limits_{k=1}^{N-1}f(x_k)+2\sum\limits_{k=1}^{N}f \left( \dfrac{ {x_{k-1}+x_k} }{ 2} \right)+\over{1}{ 2} f(x_N) \right)
mit h=b−aN, xk=a+k⋅hh = \dfrac{b-a}{N}, \ x_k=a+k\cdot h
Man sieht leicht einen Zusammenhang mit der Sehnentrapezformel QS(f)Q_S(f) und der Tangententrapezformel QT(f)Q_T(f):
Q(f)=(13)(QS(f)+2QT(f)) Q(f)=\over{1 }{ 3} \left( Q_S(f)+2Q_T(f) \right)

Fehlerabschätzung für das Restglied

Die Fehlerabschätzung für das Restglied lautet:
∣E(f)∣≤((b−a)2880)h4max⁡a≤x≤b∣f(4)(x)∣\left| E(f) \right| \le \over{(b-a) }{ 2880}h^4 \max_{a\le x \le b} {\left| f^{(4)}(x) \right|}
bzw. für reellwertige Funktionen mit einer Zwischenstelle ζ\zeta aus dem Intervall [a,b][a,b]:
E(f)=−((b−a)2880)h4f(4)(ζ)E(f)=-\over{(b-a) }{ 2880}h^4f^{(4)}(\zeta)

Siehe auch

 
 

Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.

Richard Feynman

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Simpsonsche Formel aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerische Integration