Newton-Cotes-Formeln

Eine Newton-Cotes-Formel ist eine mathematische Formel zur näherungsweisen Berechnung von Integralen. Diesen Formeln liegt die Idee zu Grunde, die zu integrierende Funktion durch ein Polynom zu interpolieren und dieses als Näherung exakt zu integrieren. Die entsprechenden Formeln sind nach den englischen Mathematikern Isaac Newton und Roger Cotes benannt.
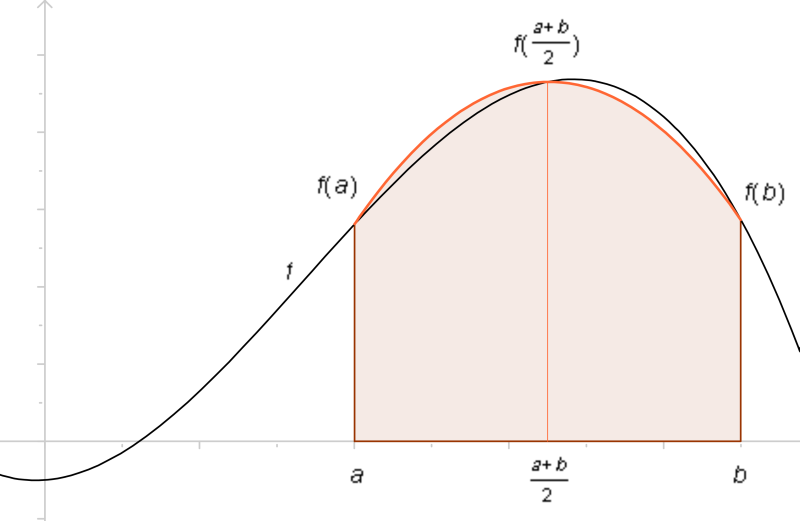
Simpson_rule.png

Definition

Zur numerischen Integration mit Hilfe einer Newton-Cotes-Formel wird das Intervall [a,b][a,b] in nn gleich große Teilintervalle unterteilt werden. Dadurch erhält man n+1n + 1 Stützstellen mit
a≤x0<x1<…<xn≤ba \leq x_0 < x_1 < \ldots < x_n \leq b
Gilt dabei a=x0a = x_0 und b=xnb = x_n, so spricht man von einer abgeschlossenen Newton-Cotes-Formel, andernfalls von einer offenen Newton-Cotes-Formel. Als Newton-Cotes-Formel selbst bezeichnet man die Summe
Q(f)=∑i=0nwif(xi)Q(f) = \sum\limits_{i=0}^n w_i f(x_i)
mit den Gewichten
wi=∫abLi(x) dxw_i = \int\limits_a^b L_i(x) \, dx
Dabei bezeichnet Li(x)L_i(x) das ii-te Lagrange-Polynom.
Li(x)=(x−x0)⋯(x−xi−1)(x−xi+1)⋯(x−xn)(xi−x0)⋯(xi−xi−1)(xi−xi+1)⋯(xi−xn)L_i(x) = \dfrac{(x-x_0)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)} {(x_i-x_0)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_n)}

Abgeschlossene Newton-Cotes-Formeln

Bei den abgeschlossenen Formeln sind die Gewichte [!symmetrisch], das heißt wn−i=wiw_{n-i}=w_i. Die folgende Tabelle listet einige Spezialfälle.
Grad nn Name Gewichte wiw_i
1 Trapezregel 1212\dfrac{1}{2} \quad \dfrac{1}{2}
2 Simpson-Regel / Keplersche Fassregel 164616\dfrac{1}{6} \quad \dfrac{4}{6} \quad \dfrac{1}{6}
3 3/8 - Regel oder auch Pulcherima 18383818\dfrac{1}{8} \quad \dfrac{3}{8} \quad \dfrac{3}{8} \quad \dfrac{1}{8}
4 Milne-Regel 790329012903290790\dfrac{7}{90} \quad \dfrac{32}{90} \quad \dfrac{12}{90} \quad \dfrac{32}{90} \quad \dfrac{7}{90}
5 192887528850288502887528819288\dfrac{19}{288} \quad \dfrac{75}{288} \quad \dfrac{50}{288} \quad \dfrac{50}{288} \quad \dfrac{75}{288} \quad \dfrac{19}{288}
6 Weddle-Regel 41840216840278402728402784021684041840\dfrac{41}{840} \quad \dfrac{216}{840} \quad \dfrac{27}{840} \quad \dfrac{272}{840} \quad \dfrac{27}{840} \quad \dfrac{216}{840} \quad \dfrac{41}{840}
Für große nn sind diese Formeln aus praktischer Sicht unbrauchbar, da viele Funktionswerte ausgewertet werden müssen. Dabei kommt es vermehrt zu Rundungsfehlern und Auslöschung. Ab n=8n=8 treten in etlichen Formeln sogar negative Gewichte auf.

Offene Newton-Cotes-Formeln

Grad nn Name Stützstellen xix_i Gewichte wiw_i
0 Mittelpunktsregel 12\dfrac{1}{2} 1
1 1434\dfrac{1}{4} \quad \dfrac{3}{4} 1212\dfrac{1}{2} \quad \dfrac{1}{2}
2 161256\dfrac{1}{6} \quad \dfrac{1}{2} \quad \dfrac{5}{6} 382838\dfrac{3}{8} \quad \dfrac{2}{8} \quad \dfrac{3}{8}
3 18385878\dfrac{1}{8} \quad \dfrac{3}{8} \quad \dfrac{5}{8} \quad \dfrac{7}{8} 1348114811481348\dfrac{13}{48} \quad \dfrac{11}{48} \quad \dfrac{11}{48} \quad \dfrac{13}{48}
 
 

Es ist unglaublich, wie unwissend die studirende Jugend auf Universitäten kommt, wenn ich nur 10 Minuten rechne oder geometrisire, so schläft 1/4 derselben sanft ein.

Georg Christoph Lichtenberg

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Newton-Cotes-Formeln aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Numerische Verfahren