Mittelwertsatz der Integralrechnung

Satz 15VJ (Mittelwertsatz der Integralrechnung)

Sei ff eine auf dem Intervall [a,b][a,b] stetige Funktion. Dann gibt es ein x0∈[a,b]x_0\in[a,b] mit:
∫abf(x)d⁡x=(b−a)f(x0)\int\limits_a^bf(x)\d x=(b-a)f(x_0)

Geometrische Deutung

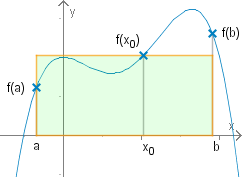
MwInt.png
Wir können immer ein x0∈[a,b]x_0\in[a,b] finden, so dass der Flächeninhalt unter der Kurve zwischen aa und bb dem eines Rechtecks mit den Seitenlängen b−ab-a und f(x0)f(x_0) entspricht.

Beweis

Nach Satz 16MA ist f([a,b])f([a,b]) ein Intervall.
Nach Satz 15FV nimmt ff auf [a,b][a,b] das Minimum mm und das Maximum MM an. Es gilt:
m(b−a)≤sfm(b-a) \leq s_f=∫abf(x)d⁡x = \int\limits_a^bf(x)\d x=Sf≤M(b−a)=S_f\leq M(b-a),
also
m≤1b−a∫abf(x)d⁡x≤Mm\leq\dfrac 1 {b-a} \int\limits_a^b{f(x)\d x}\leq M.
Nach dem Zwischenwertsatz muss es dann ein x0x_0 geben, mit f(x0)=1b−a∫abf(x)d⁡xf(x_0)= \dfrac 1 {b-a}\int\limits_a^bf(x)\d x. □\qed
 
 

Das entscheidende Kriterium ist Schönheit; für häßliche Mathematik ist auf dieser Welt kein beständiger Platz.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen