Problem des Handlungsreisenden

Das Problem des Handlungsreisenden (engl. Traveling Salesman Problem, kurz TSP) ist ein kombinatorisches Optimierungsproblem des Operations Research und der theoretischen Informatik. Die Aufgabe besteht darin, eine Reihenfolge für den Besuch mehrerer Orte so zu wählen, dass die gesamte Reisestrecke des Handlungsreisenden nach der Rückkehr zum Ausgangsort möglichst kurz ist.

Mathematische Beschreibung

Modellierung als Graph

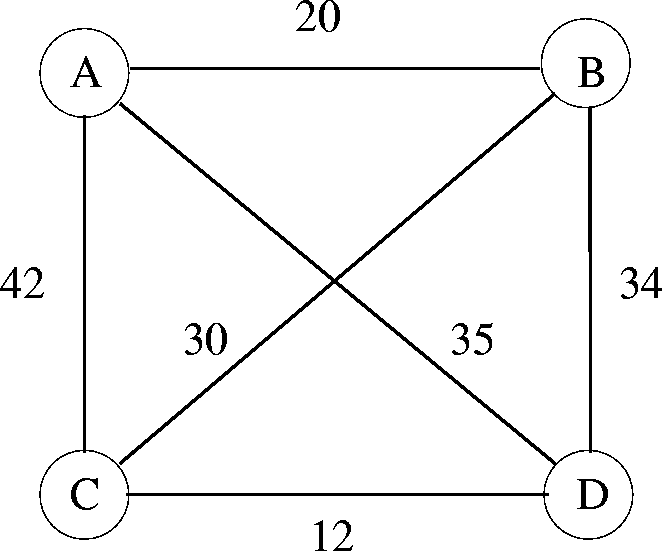
Weighted_K4.png
Symmetrisches TSP auf 4 Städten
Damit mathematische Verfahren zur Lösung verwendet werden können, muss eine reale Situation zunächst durch ein einfaches Modell abgebildet werden. Das Problem des Handlungsreisenden lässt sich mit Hilfe eines Graphen anschaulich modellieren, das heißt: durch Knoten und Kanten. Dabei repräsentieren die Knoten (im Bild: A bis D) die Städte, während sich jede Kante (i,j)(i,j) zwischen zwei Knoten ii und jj zusammen mit ihrer Länge cij≥0c_{ij} \geq 0 je nach Zusammenhang beispielsweise als geographische Länge einer Verbindung, als Reisezeit oder als Kosten einer Reise zwischen zwei Städten interpretieren lässt. Eine Tour (auch Hamiltonkreis genannt) ist ein Kreis in diesem Graphen, der jeden Knoten genau einmal enthält. Ziel ist es, eine möglichst kurze Tour zu finden.
Um die Untersuchung des Problems zu vereinfachen und um sicherzustellen, dass es eine Tour gibt, wird meist angenommen, dass der Graph vollständig ist, dass also zwischen je zwei Knoten immer eine Kante existiert. Dies lässt sich dadurch erreichen, dass überall dort, wo keine Kante existiert, eine künstliche, sehr lange Kante eingefügt wird. Aufgrund ihrer hohen Länge wird eine solche Kante nie in einer kürzesten Tour vorkommen, es sei denn, es gäbe sonst keine Tour.
Je nach Eigenschaften der Kantengewichte werden noch unterschiedliche Spezialfälle des Problems unterschieden, von denen die wichtigsten das symmetrische und das metrische TSP sind.

Symmetrisches TSP

Beim allgemeinen asymmetrischen TSP können die Kanten in Hin- und Rückrichtung unterschiedliche Länge haben, so dass dieses Problem mit Hilfe eines gerichteten Graphen modelliert werden muss. Er reicht also nicht, bloß von der Verbindung zwischen zwei Knoten und ihrer Länge zu sprechen, zusätzlich muss noch die Richtung angegeben werden.
Beim symmetrischen TSP dagegen sind für alle Knotenpaare (i,j)(i,j) die Kantenlängen in beide Richtungen identisch, d. h. es gilt cij=cjic_{ij} = c_{ji}. Als Konsequenz davon hat jede Tour in beide Richtungen dieselbe Länge. Die Symmetrie halbiert also die Anzahl der möglichen Touren. Ein symmetrisches TSP wird üblicherweise mit Hilfe eines ungerichteten Graphen modelliert (wie im Bild). Ein Traveling Salesman Problem zwischen realen Städten kann asymmetrisch oder symmetrisch sein, je nachdem, ob beispielsweise durch Baustellen oder Einbahnstraßen der Weg in eine Richtung länger dauert als in die andere oder nicht.

Metrisches TSP

Ein symmetrisches TSP heißt metrisch, wenn zusätzlich seine Kantenlängen die Dreiecksungleichung erfüllen. Anschaulich bedeutet dies, dass sich Umwege nicht lohnen, weil die direkte Verbindung von ii nach jj nie länger ist als der Weg von ii nach jj über einen dritten Knoten kk:
cij≤cik+ckjc_{ij} \le c_{ik} + c_{kj}
Solche Kantenlängen definieren eine metrische Distanzfunktion auf der Knotenmenge, also ein Entfernungsmaß, das die intuitiv von einem Abstand erwarteten Bedingungen erfüllt. Mehrere in der Praxis häufig auftretende Distanzfunktionen sind metrisch, erfüllen also die Dreiecksungleichung:
  • die euklidische Metrik des euklidischen TSP,
  • die Manhattan-Metrik (auch City-Block-Metrik) des rektilinearen TSP, bei der die Distanz zwischen zwei Knoten eines gitterförmigen Graphen (wie dem Straßennetz von Manhattan) die Summe der Entfernungen in x- und y-Richtung ist,
  • oder die Maximums-Metrik, bei der die Distanz zwischen zwei Knoten eines gitterförmigen Graphen das Maximum der Entfernungen in x- bzw. y-Richtung ist.
Die letzten beiden Metriken finden beispielsweise Anwendung beim Bohren von Leiterplatten, wo ein Bohrer, der eine vorgegebene Menge von Löchern in möglichst kurzer Zeit abarbeiten muss, in beide Dimensionen unabhängig bewegt werden kann, um von einem Loch zum nächsten zu gelangen. Die Manhattan-Metrik entspricht dem Fall, dass die Bewegung in beide Richtungen nacheinander erfolgt, während bei der Maximum-Metrik beide Bewegungen gleichzeitig erfolgen und die Gesamtzeit von der jeweils längeren Strecke in x- bzw. y-Richtung bestimmt wird.
Distanzen, die aus Entfernungstabellen in Straßenkarten entnommen werden, sind nicht notwendigerweise metrisch, weil dort oft die km-Länge eines zeitlich kürzesten Weges angegeben ist, der nicht unbedingt ein kürzester Weg bzgl. der Reisestrecke ist. Falls es im praktischen Planungsproblem zulässig ist, Orte mehrfach zu besuchen, kann man das Problem auf ein metrisches TSP im sogenannten Distanzgraphen reduzieren. Dort entspricht die Kantenlänge zwischen zwei Knoten ii und jj der Länge eines kürzesten i−ji-j-Weges bzgl. der ursprünglichen Kantenlängen cijc_{ij}. Die so definierten neuen Kantenlängen erfüllen immer die Dreiecksungleichung.

Modellierung als ganzzahliges lineares Programm

Ein Ansatz zur Lösung des Problems ist die Formulierung als ganzzahliges lineare Programm, in dem die Entscheidungen durch Variablen und die Bedingungen durch lineare Ungleichungen beschrieben werden. Hierfür gibt es mehrere mögliche Varianten. Beispielhaft soll hier eine Modellierung für das symmetrische TSP mit Knotenmenge VV vorgestellt werden. Für jede Kante {i,j}\{i,j\} wird eine binäre Variable xij∈{0,1}x_{ij} \in \{0,1\} eingeführt, die für eine gegebene Tour angibt, ob die Kante {i,j}\{i,j\} in dieser Tour enthalten ist (xij=1)(x_{ij} = 1) oder nicht (xij=0)(x_{ij} = 0). Jede Tour lässt sich auf diese Art durch Angabe der zugehörigen Variablenwerte angeben, aber nicht jede 0-1-Belegung der Variablenwerte definiert eine Tour.
Die Bedingungen dafür, dass eine Variablenbelegung eine Tour definiert, lassen sich durch lineare Ungleichungen ausdrücken, von denen allerdings nicht alle bekannt sind. Im folgenden sollen daher beispielhaft zwei einfache Typen von Ungleichungen vorgestellt werden, die ein Vektor xx auf jeden Fall erfüllen muss, damit er eine Tour beschreibt. Sie lassen sich daher als Teil einer Relaxierung in einem Schnittebenenverfahren zur Lösung des Problems nutzen.
TSP_degree_constraints.png
Gradbedingung: In jeden Knoten i muss genau eine Kante der Tour hinein- bzw. hinausgehen.
Jeder Knoten muss über genau zwei Tourkanten mit den restlichen Knoten verbunden sein, nämlich durch eine hinein- und eine hinausführende Kante:
: ∑j∈V∖{i}xij=2(1)\sum\limits_{j \in V \setminus \{i\}} x_{ij} = 2 \qquad (1)
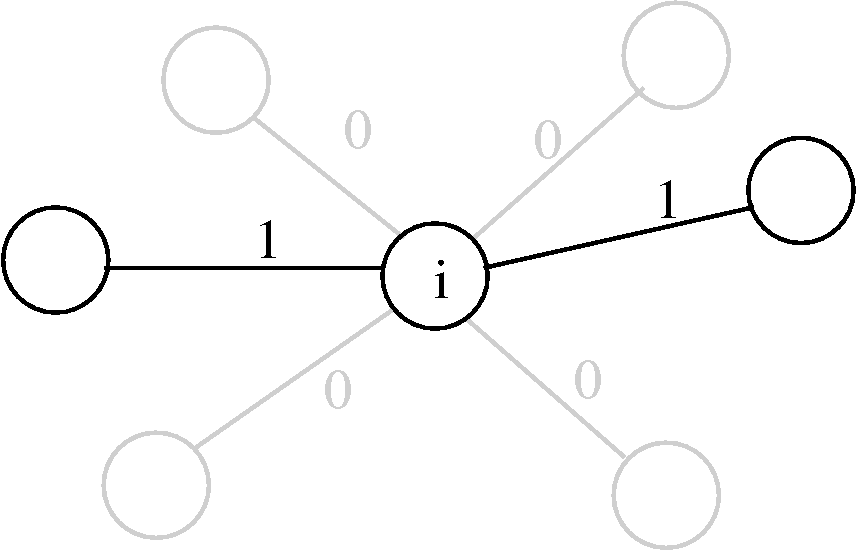
für alle i∈Vi \in V. In der Summe ist jeder Summand xijx_{ij} entweder 1 (in der Tour enthalten) oder 0 (nicht enthalten). Die Summe zählt daher genau die Zahl der Kanten der Tour, die den Knoten ii als Endknoten haben. Sie muss den Wert 2 annehmen, da jeweils eine Kante hinein- und hinausführen muss. Im nebenstehenden Bild ist ein Knoten ii mit ein- und ausgehenden Kanten dargestellt, wobei die Tourkanten fett gekennzeichnet sind. An den Kanten stehen die Werte xijx_{ij}, die zu den oben genannten Summen beitragen.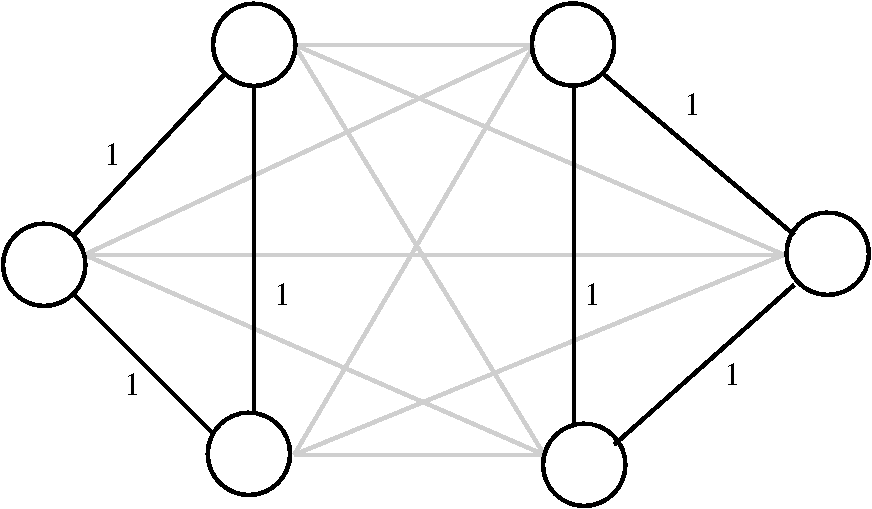
TSP_short_cycles.png
Kurzzyklen: Diese Variablenbelegung erfüllt alle Gradbedingungen, definiert aber keine Tour.
Die obige Bedingung wird nicht nur von Touren erfüllt, sondern auch von Variablenbelegungen, die mehrere getrennte Kreise (sogenannte Kurzzyklen) beschreiben, wobei jeder Knoten in genau einem Kreis enthalten ist (siehe Bild). Um so etwas auszuschließen, müssen noch Kurzzyklusungleichungen (auch Subtour-Eliminationsbedingungen genannt) erfüllt werden. Sie besagen, dass jede Knotenmenge S⊂VS \subset V, die weder leer ist noch alle Knoten enthält, durch mindestens zwei Kanten der Tour mit den restlichen Knoten verbunden sein muss:
: ∑i∈S, j∉Sxij≥2(2)\sum\limits_{i \in S, \, j \notin S} x_{ij} \geq 2 \qquad (2)
für alle Knotenmengen SS mit 1≤∣S∣≤∣V∣−11 \leq |S| \leq |V|-1. Die Summe zählt alle Kanten der Tour zwischen einem Knoten i∈Si \in S und einem anderen Knoten j∉Sj \notin S. Zur Vermeidung redundanter Ungleichungen kann man sich auch auf Knotenmengen SS mit mindestens zwei und höchstens ∣V∣−2|V|-2 Knoten beschränken. Im nebenstehenden Bild sind wieder die Kanten {i,j}\{i,j\} mit xij=1x_{ij} = 1 fett gezeichnet, während die übrigen Kanten den Wert xij=0x_{ij} = 0 haben. Das Hinzufügen der Bedingung (2) für die Knotenmenge SS, die aus den drei linken Knoten besteht, würde dafür sorgen, dass S durch mindestens zwei Tourkanten mit den drei rechten Knoten verbunden sein muss, und damit die beiden gezeigten Kurzzyklen ausschließen.
Die Zahl der Ungleichungen vom Typ (2) wächst exponentiell mit der Anzahl der Städte, da fast jede der 2∣V∣2^{|V|} Teilmengen von Knoten eine Ungleichung definiert. Dieses Problem kann aber mit Hilfe von Schnittebenenverfahren umgangen werden, bei denen diese Ungleichungen erst dann hinzugefügt werden, wenn sie tatsächlich gebraucht werden.
Ziel ist es, unter allen Touren eine kürzeste zu finden:
: min⁡ {∑i∈V∑j∈V∖{i}cijxij∣x\min \, \{ \sum\limits_{i \in V} \sum\limits_{j \in V \setminus \{i\}} c_{ij} x_{ij} | x definiert eine Tour} (3)\}\, \qquad (3)
Da die Variablen xijx_{ij} nur die Werte 0 oder 1 annehmen, zählt die Summe genau die Längen cijc_{ij} der Kanten {i,j}\{i,j\} zusammen, die in der Tour enthalten sind.
Man kann zeigen, dass die meisten der Bedingungen (1) und (2) Facetten des TSP-Polytops definieren, d. h. dass sie zu den besten linearen Ungleichungen gehören, die es zur Beschreibung einer Tour geben kann. Allerdings reichen sie nicht aus, d. h. es gibt Vektoren xx, die alle diese Ungleichungen erfüllen, aber trotzdem nicht zu einer Rundreise gehören.

Algorithmische Komplexität

Bei der Suche nach einer Lösung für das Problem des Handlungsreisenden ist eine der wohl grundlegendsten Fragen die nach der Anzahl der möglichen Rundreisen. In jedem Knoten der Tour stehen dem Handlungsreisenden jeweils alle Städte zur Auswahl, die er noch nicht besucht hat. Da der Ausgangspunkt beliebig ist, ergeben sich insgesamt (n−1)!(n-1)! mögliche Touren für ein asymmetrisches und (n−1)!/2(n-1)!/2 Touren für ein symmetrisches TSP.
Das Problem des Handlungsreisenden ist NP-vollständig, auch wenn eine bestimmte Metrik vorausgesetzt wird. Dies verhindert unter der bisher unbewiesenen, aber allgemein vermuteten Annahme, dass die beiden Komplexitätsklassen P und NP nicht identisch sind, die Existenz eines polynomialen Lösungsalgorithmus. Anschaulich bedeutet dies, dass die Laufzeit jedes deterministischen Algorithmus zur optimalen Lösung dieses Problems exponentiell mit der Anzahl der Städte steigt, so dass ein solcher Algorithmus aus theoretischer Sicht „nicht wesentlich“ besser sein kann als das Ausprobieren aller möglichen Touren, was schon bei kleinen Städtezahlen nicht mehr durchführbar ist. Beispielsweise gibt es für das symmetrische TSP mit 15 Städten über 43 Milliarden mögliche Rundreisen, bei 18 Städten sind es schon über 17 Billionen.
Darüber hinaus wird die Suche nach guten Lösungen dadurch erschwert, dass das Problem des Handlungsreisenden (unter der Annahme P ≠\neq NP) nicht einmal in polynomialer Laufzeit beliebig gut approximierbar ist. Man findet also nicht zu jedem beliebig kleinen ϵ>0\epsilon >0 einen polynomialen Algorithmus ALG, der für jedes TSP-Problem G eine Tour berechnet, deren Länge höchstens um den Faktor 1+ϵ1 + \epsilon vom Optimalwert abweicht:
OPT(G)≤ \leq ALG(G)≤(1+ϵ) \leq (1+\epsilon)OPT(G)
OPT(G) bezeichnet dabei die Länge einer optimalen Tour, ALG(G) die der vom Algorithmus berechneten.
Weiter oben wurden allerdings bereits zwei Heuristiken vorgestellt, die für metrische TSP und bestimmte ϵ\epsilon eine Gütegarantie von 1+ϵ1+\epsilon geben, nämlich die Minimum-Spanning-Tree-Heuristik mit ϵ=1\epsilon=1 und die Christofides-Heuristik mit ϵ=\epsilon=1/2. Bisher ist kein Algorithmus mit einer besseren Gütegarantie als 1/2 bekannt, genauso wenig wie ein ϵ\epsilon-approximativer Algorithmus für allgemeine, nicht-metrische TSP.

Lösungsverfahren

Die bekannten Lösungsverfahren unterteilen sich in zwei Gruppen, die miteinander kombiniert werden können. Exakte Lösungsverfahren finden – beliebig lange Laufzeit vorausgesetzt – grundsätzlich eine beweisbare Optimallösung. Heuristische Verfahren finden oft in kurzer Zeit gute Lösungen, die aber im allgemeinen Fall beliebig schlecht sein können. Für das metrische TSP gibt es allerdings polynomiale Heuristiken, deren Lösungen grundsätzlich höchstens um den Faktor 1,5 bzw. 2 länger sind sind als eine kürzeste Rundreise.

Exakte Lösungsverfahren

Ein exaktes Verfahren, das aber aufgrund der vielen möglichen Touren pratisch nicht durchführbar ist, ist die Aufzählung aller möglichen Touren. Mit Methoden der ganzzahligen linearen Optimierung, insbesondere Branch-and-Cut, lassen sich dagegen Instanzen in praktisch relevanten Größenordnungen beweisbar optimal lösen, oder zumindest die Güte einer gefundenen Tour im Vergleich zu einer Optimallösung abschätzen.
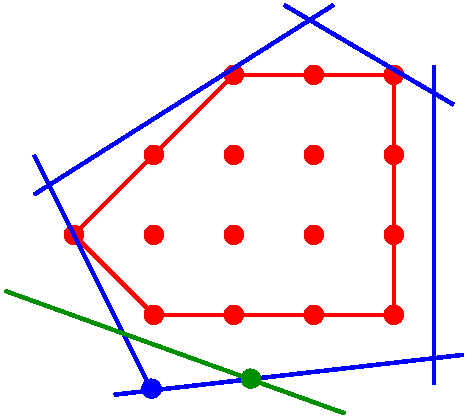
Cutting_plane_algorithm2.png
Schnittebene schneidet eine unzulässige Lösung (blauer Punkt) vom roten Polytop der zulässigen ganzzahligen Punkte ab. Die nächste Iteration wird den (ebenfalls unzulässigen) grünen Punkt als Lösung liefern, der näher am roten Polytop liegt als der abgeschnittene blaue Punkt.
Geometrisch interpretiert, betrachten diese Verfahren das Problem als konvexes Polytop, also als mehrdimensionales Vieleck im nn-dimensionalen Raum, wobei nn die Anzahl der Kanten des Graphen ist. Dieses Polytop ist ein Teil des Einheitswürfels [0,1]n[0,1]^n, von dem durch Ungleichungen Teile abgeschnitten wurden (etwa wie von einem Stück Käse). Wie oben beschrieben, repräsentiert jede Ecke dieses Einheitswürfels (also jeder Vektor, der nur aus 0/1-Einträgen besteht) eine Tour, sofern sie bestimmte lineare Ungleichungen erfüllt. Die beschriebenen Ungleichungen schneiden also genau die Ecken des Einheitswürfels ab, die keine Tour darstellen. Beispielsweise schneiden Ungleichungen vom Typ (1) unter anderem den Nullvektor (0,...,0) ab, der einer (unmöglichen) Tour ohne Kanten entsprechen würde. Übrig bleibt ein Polytop PP, bei dem jede ganzzahlige Ecke eine Tour beschreibt. Ziel ist es also, eine 0/1-Ecke von PP mit minimalem Zielfunktionswert (3) zu finden.
Im nebenstehenden Bild ist das Polytop PP der zulässigen ganzzahligen Lösungen rot eingezeichnet. Die Minimierung der Zielfunktion entspricht dem Finden einer Ecke von PP, die möglichst weit links unten im Bild liegt. Da dieses Polytop nicht genau bekannt ist, wird stattdessen ein größeres Polytop (im Bild blau) betrachtet, das einfacher zu behandeln ist und PP enthält. Durch Lösen vieler linearer Programme, Abschneiden nicht benötigter Teile des größeren Polytops mit Hilfe von Schnittebenen sowie durch Aufteilung in mehrere Teilpolytope mit Hilfe von Branch-and-Bound wird versucht, eine optimale Ecke des inneren Polytops zu bestimmen. Im Bild ist eine grüne Schnittebene dargestellt, die den unzulässigen blauen Punkt vom inneren Polytop PP trennt und einen Teil des äußeren, blauen Polytops abschneidet. Dieser Vorgang entspricht dem Hinzufügen einer neuen Ungleichung, z. B. vom Typ (2), im ganzzahligen linearen Programm. Eine genauere Beschreibung dieser Verfahren ist im Artikel Ganzzahlige lineare Optimierung zu finden.
Die alleinige Anwendung dieser Verfahren reicht meist nicht aus, um schnell gute Rundreisen zu finden. Ihr Hauptvorteil liegt darin, dass sie Angaben liefern, wie lang eine kürzeste Tour mindestens sein muss. Mit einer solchen unteren Schranke für den optimalen Lösungswert lässt sich abschätzen, wie gut eine gefundene Tour im Vergleich zu einer optimalen Rundreise ist, ohne diese zu kennen. Hat man beispielsweise eine untere Schranke von 100 und eine Tour der Länge 102 gefunden, beträgt der so genannte Optimalitätsgap, also der relative Abstand zwischen unterer Schranke und kürzester bekannter Tourlänge, (102-100)/100 = 2.Dae∈eoptima≤Tourνrzwischen100und102lie≥nka∩,ka∩der≥funde≠Lo¨sungswert102ebenfallsho¨chstens2\displaystyle{.{D}{a}{e}\in{e}{o}{p}{t}{i}{m}{a}\le{T}{o}{u}{r}\nu{r}{z}{w}{i}{s}{c}{h}{e}{n}{100}{u}{n}{d}{102}{l}{i}{e}\ge{n}{k}{a}\cap,{k}{a}\cap{d}{e}{r}\ge{f}{u}{n}{d}{e}\ne{L}ö{s}{u}{n}{g}{s}{w}{e}{r}{t}{102}{e}{b}{e}{n}{f}{a}{l}{l}{s}{h}ö{c}{h}{s}{t}{e}{n}{s}{2}} vom Optimalwert entfernt sein. Wenn die Länge einer gefundenen Tour genauso groß ist wie die untere Schranke, ist damit bewiesen, dass die gefundene Lösung optimal ist. Um gute Touren zu finden, können diese exakten Verfahren mit Heuristiken kombiniert werden, von denen einige im nachfolgenden Abschnitt beschrieben werden.

Heuristiken

Um schnell zu brauchbaren Lösungen zu kommen, sind meist Heuristiken, also Näherungsverfahren, notwendig, die aber in der Regel keine Güteabschätzung für die gefundenen Lösungen liefern. Je nachdem, ob eine Heuristik eine neue Tour konstruiert oder ob sie versucht, eine bestehende Rundreise zu verbessern, wird sie als Eröffnungs- (auch Konstruktions-) oder Verbesserungsverfahren bezeichnet.

Eröffnungsverfahren

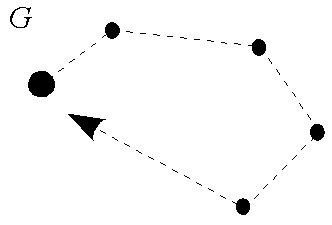
Nearest_Neighbor_Heuristik.png
Nearest-Neighbor-Heuristik
Dem intuitiven Vorgehen eines Handlungsreisenden entspricht wohl am ehesten die Nearest-Neighbor-Heuristik (nächster Nachbar). Von einer Stadt ausgehend wählt diese jeweils die nächstgelegene als folgenden Ort aus. Dieses wird sukzessive fortgesetzt, bis alle Städte bereist wurden und der Handlungsreisende zum Ausgangsort zurückgekehrt ist. In jeder Stadt muss also der kürzeste ausgehende Weg gesucht werden. Maximal kann es pro Stadt nur so viele ausgehende Kanten geben, wie Knoten im Graphen vorhanden sind. Daraus ergibt sich eine algorithmische Komplexität von O(n²), die Anzahl der Rechenschritte hängt also quadratisch von der Zahl der Städte ab. Dass diese Heuristik im Allgemeinen jedoch nicht die beste Lösung liefert, liegt daran, dass die Distanz zwischen der Ausgangsstadt und der letzten besuchten Stadt bis zuletzt nicht berücksichtigt wird. Die Nearest-Neighbor-Heuristik kann beliebig schlechte Ergebnisse liefern, das heißt, es gibt keinen konstanten, instanzunabhängigen Approximationsfaktor für den Lösungswert im Vergleich zum Optimalwert.
Ein ganze Klasse weiterer Eröffnungsverfahren bilden die sogenannten Einfüge-Heuristiken. Die einfachsten Varianten davon sind die Nearest-Insertion-Heuristik (nächste Einfügung) und die Farthest-Insertion-Heuristik (entfernteste Einfügung). Gegeben seien (wenige) einander benachbarte Städte, für die sich durch exakte Verfahren schnell eine optimale Rundreise ermitteln lässt. Nun wird schrittweise überprüft, welche noch nicht besuchte Stadt am nächsten (beziehungsweise am entferntesten) zu einer der Verbindungslinien der bisherigen Rundreise liegt. Ist diese Stadt gefunden, so wird sie zwischen den ihr am nächsten liegenden Städten in die Tour eingebaut. Das Verfahren wird solange fortgesetzt, bis die Rundreise alle Städte umfasst. Auch die Lösungen dieser Heuristik können im Vergleich zu einer Optimallösung beliebig schlecht sein.
Eine andere Klasse von Heuristiken unterteilt die Knotenmenge in einzelne Partitionen (z. B. nach geographischen Kriterien), die jeweils teiloptimiert werden. Anschließend werden die Teillösungen zu einer Gesamtlösung kombiniert. Diese ist in der Regel nur lokal optimal und kann gegenüber dem globalen Optimum beliebig schlecht sein.
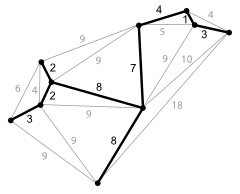
Minimum_spanning_tree.png
Minimal aufspannender Baum
Die Minimum-Spanning-Tree-Heuristik (MST) berechnet zunächst einen minimal aufspannenden Baum, also einen Graphen, in dem alle Punkte miteinander verbunden sind und der minimale Länge besitzt. Davon ausgehend wird eine Tour konstruiert, indem zunächst alle Baumkanten verdoppelt werden und danach eine Eulertour in dem entstandenen eulerschen Graphen gesucht wird. Diese wird zuletzt durch direkte Kanten abgekürzt, falls Knoten doppelt besucht werden. Im Falle eines metrischen TSP kann man zeigen, dass die so konstruierte Tour höchstens doppelt so lang ist wie eine kürzeste Tour.
Eine noch bessere Approximationsgüte für metrische TSP wird durch die Christofides-Heuristik erreicht. Mit ihr kann eine Rundreise berechnet werden, die höchstens eineinhalb mal so lang wie eine optimale ist. Hierbei wird statt der Verdopplung der Kanten in der MST-Heuristik eine kleinste perfekte Paarung auf den Knoten ungeraden Grades im minimal aufspannenden Baum berechnet, um einen eulerschen Graphen zu erzeugen. Dieser Algorithmus ist jedoch aufwändiger.

Verbesserungsverfahren

Verbessernde Optimierungsverfahren, auch Post-Optimization-Verfahren (Nach-Optimierung) versuchen, eine bestehende Tour durch kleine Modifikationen zu verkürzen. Führt keine der betrachteten Änderungen mehr zu einer Verbesserung, so ist ein lokales Optimum gefunden (aber nicht notwendigerweise ein globales). Die k-Opt-Heuristiken verfolgen diesen Ansatz, indem sie systematisch Gruppen von kk Kanten aus der Tour entfernen und durch kk andere Kanten ersetzen, so dass wieder eine Tour entsteht. Problematisch bei solchen Verfahren wird jedoch schnell die Tatsache, dass bei einer vollständigen Durchführung der Aufwand im Vergleich zur Aufzählung aller möglichen Touren nicht gesenkt würde. In praktischen verwendeten Implementierungen ist kk daher üblicherweise höchstens 5. Dabei werden oft alle Austauschmöglichkeiten von zwei und drei Kanten durchprobiert, während Kantenaustausche von mehr als drei Kanten wegen des Rechenaufwandes nur noch sehr sparsam eingesetzt werden.
Die Güte einer k-Opt-Heuristik in der Praxis hängt stark von der Auswahl der auszutauschenden Kanten und des Parameters kk ab, für die es verschiedene heuristische Kriterien gibt.

Metaheuristische Verfahren

Metaheuristiken kombinieren lokale und globale Suchverfahren in einer abstrakten Strategie für die heuristische Optimierung eines Problems. Viele dieser Verfahren berechnen eine heuristische Startlösung (beispielsweise mit der Nearest-Neighbour-Heuristik) und verbessern diese solange durch ein lokales Suchverfahren, wie z. B. K-Opt-Heuristiken, bis keine bessere Tour mehr gefunden wird. Durch Tabu-Listen wird vermieden, dass bereits gefundene Touren nochmal betrachtet werden. Um das Steckenbleiben in lokalen Minima zu verhinden, kann man beispielsweise
  • mehrere Versuche starten (Bergsteigeralgorithmus),
  • zwischendurch erst größere, später nur noch kleinere Verschlechterungen akzeptieren (Simulierte Abkühlung (engl. simulated Annealing, auch Sintflutalgorithmus genannt)),
  • mehrere bereits gefundene Touren zu einer neuen Tour kombinieren oder Touren zufällig verändern (evolutionäre und genetische Algorithmen).
Eine ganze Klasse weiterer naturinspirierter Verfahren verwendet Schwarmintelligenzen. Bei so genannten Ameisenalgorithmen (engl. Ant Colony Optimization), wird hierzu das natürliche Verhalten von Ameisen auf der Wegsuche modelliert, während bei der Partikelschwarmoptimierung (engl. Particle Swarm Optimization) das Verhalten von Vogel- oder Fischschwärmen als Vorbild genommen wird. Auch mit künstlichen neuronalen Netzen und ähnlichen statistischen Verfahren lassen sich effizient brauchbare Lösungen finden. Modelle wie das Hopfield-Netz oder selbstlernende Netze (Self-Organizing Maps) können durch ihren Aufbau viele Aspekte des TSP abbilden. Der große Nachteil künstlicher neuronaler Netze ist aber, dass oft nur lokale Minima gefunden werden.
Generell hängen der Erfolg und die Laufzeit metaheuristischer Verfahren wesentlich von der Definition und Implementierung der einzelnen Schritte ab. Prinzipiell können all diese Verfahren gute Lösungen berechnen, aber auch beliebig schlecht im Vergleich zu einer Optimallösung sein, sofern nicht zur Berechnung der Startlösung eine Heuristik mit Gütegarantie verwendet und deren Wert dann später nie mehr überschritten wird. Sie können aber sinnvoll z. B. im Rahmen eines Branch-and-Cut-Algorithmus eingesetzt werden.

Duale Heuristiken

Das Problem des Handlungsreisenden ist eines der wenigen kombinatorischen Optimierungsprobleme, bei dem sich auf einfache Weise brauchbare untere Schranken für die minimale Länge einer Tour (allgemein: die minimalen Kosten einer Lösung) angeben lassen. Da beispielsweise jede Tour, auch eine optimale, genau nn Kanten enthält, muss sie mindestens so lang sein wie die Summe der nn kleinsten Kantenlängen. Eine andere untere Schranke ergibt sich aus der Beobachtung, dass beim Löschen einer beliebigen Kante aus einer Tour ein aufspannender Baum entsteht, also ein Teilgraph, der alle Knoten, aber keine Kreise enthält. Die Tour ist mindestens so lang wie dieser Baum und damit per Definition auch mindestens so lang wie ein minimal aufspannender Baum (also ein aufspannender Baum mit minimaler Summe der Kantenlängen), der sich leicht bestimmen lässt. Da dies für jede Tour gilt, liefert die Länge eines minimal aufspannenden Baums eine untere Schranke für die Länge einer optimalen Tour.

Praktische Grenzen der Berechenbarkeit

Die größte Instanz eines (symmetrischen) Rundreiseproblems, die bisher nachweisbar optimal gelöst wurde, ist ein Planungsproblem für das Layout integrierter Schaltkreise mit 33.810 Knoten. Dieser Rekord wurde im Jahre 2005 von William Cook und anderen mit Hilfe einer Kombination aus verschiedenen Heuristiken und dem Branch-and-Cut-basierten Programm Concorde aufgestellt, wobei frühere Teilergebnisse verschiedener universitärer Arbeitsgruppen als Grundlage verwendet wurden. Die bis dahin größte optimal gelöste Instanz bestand aus 24.978 schwedischen Städten, gelöst im Jahre 2004. Mit Hilfe spezieller Dekompositionstechniken und dem Einsatz mehrerer paralleler Computer haben William Cook u. a. Lösungen für ein TSP auf über 526 Millionen Sternen gefunden, die nachweislich höchstens 0,798 % vom Optimum entfernt sind.
Aus der Tatsache, dass ein TSP einer bestimmten Größe optimal gelöst werden konnte, folgt jedoch nicht, dass jede Instanz dieser Größe optimal gelöst werden kann, da – wie bei den meisten kombinatorischen Optimierungsproblemen – die Schwierigkeit der Lösung stark von den Eingabeparametern (in diesem Fall den Kantengewichten) abhängt. Bei TSPs, die aus praktischen Anwendungen entstehen, müssen oft noch weitere Nebenbedingungen, wie beispielsweise Zeitfenster, berücksichtigt werden. Daher sind in der Regel die größten optimal lösbaren Probleminstanzen solcher Varianten deutlich kleiner als beim klassischen Problem des Handlungsreisenden, so dass in der Praxis oft auf heuristische Ansätze zur Lösung zurückgegriffen wird. Kombinationen von heuristischen Verfahren mit LP-basierten Verfahren wie Branch-and-Cut werden vor allem im Forschungsumfeld eingesetzt, um mit Hilfe unterer Schranken für die Tourlänge die Qualität von Lösungen und Lösungsverfahren beurteilen zu können.
 
 

Wie ist es möglich, daß die Mathematik, letztlich doch ein Produkt menschlichen Denkens unabhängig von der Erfahrung, den wirklichen Gegebenheiten so wunderbar entspricht?

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Problem des Handlungsreisenden aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Graphentheorie